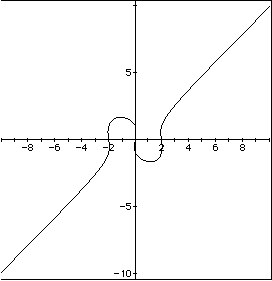
I noticed that the graph has a has a "s" shape to it as it
approaches the origin. It crosses the x axis at 2 and -2 . It crosses the
y axis at 1 and -1.
Now I am going to replace 4 with another number
It appears that by changing the 4 to a smaller number it has caused the
"s" shape to shrink.
Questions: What is happening to the max. and min. of the "s"?
What happens if I put in a lager number, does that increase the size of
the "s"? So I increased the 4 to 5. When the 4 is increased to
5 the "s" does increase in size.
Question: How much will it increase and will it lose it's shape? When you
put in "s " fraction , then compare 4 and 4.5,what happens to
the "s"?
When I tried 4.5, the "s" was not increased. The 4.5 "s"
was smaller and changes shape some.
Question: What happens with 4 and 3.5? I would think that it might be lager
than the 4. But it too was smaller and distorted.
Now I am wondering if I put a number like 8.5 will it be lager or smaller.
My guess is that it will be smaller because of the fraction. My first graph
of 4 and the 8.5 looked the same, this was kind of confusing. I tried 9.5.
With 9.5 the "s" goes back out side I am going to compare 9 and
9.5
The 9's "s" is larger than the 9.5's "s" which is larger
than the 4 "s"
Question: When does this fractional change takes place?
The 4.5 was smaller than the 4 and then the 8.5 was the same as the 4 then
the 9.5 was larger than the 4. I would like to look at the values between
9.5 and 4.5 Strange, 5.5 went between 4 and 4.5.
Question: Where will 6.5 go.
The "s" of the 6.5 went between 5.5 and 4. Now I am guessing that
7.5 goes between 6.5 and 4. When I tried the 7.5 that is exactly what happened.
I now understand why when I graphed 4 and 8.5 they where the same graph.
I am sure this could be prove with algebra. But instead of getting into
that I would like to see if I change the fractional part what happens.
I will look at "s"=4.25. It has appeared to have closed up the
"s".
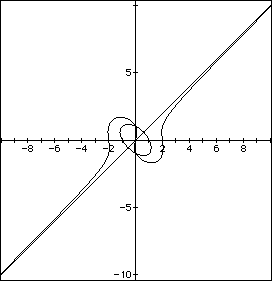
This is the graph of 4 with the "s" shape and 4.25 with the
closed up "s" that looks like a circle around a straight line.
Question: What happens at 5.25, 6.25, and 8.25?
They just seem to be approaching the 4 again, so I will look at 3.25 and
2.25.
This looked like the "s" that formed the circle pulled apart
Next, I compared 3.25 to 8.25 together.
It was a very interesting progression.
Question: I would like to know what number "m.25" would it take
for the graph to go on the outside of "s" of 4?
After a couple of tries, I found out that 16.25 and 4 had the same graph
I am assuming that 17.25 will make the graph go on the out side.
It did make it go on the outside in a big move. Looking back at the 4 and
the 8.5 having the same graph and the 4 and 16.25 having the same graph.
I am not sure why this is but I am going to see if 4 and 20.75 have the
same graph.
The graphs where not the same. It might be 4 and 20 but I must go on to.
I will try adding a constant to both a side. The first constant I will add
will be 3 to the left side.
When comparing the graph with 4 and the graph of 3 being added to the left
side we notice that this has caused a small distorted circle to from in
one region of the "s". Now I would like to try adding to the right
hand side.
This caused a small circle to be formed in the other region of the "s".
I would like to look at several different values being added to the left
hand side to see when this circle is formed.
These are the graphs of 1,2,and 3 being added to the left side.
The circle is formed between 2 and 3. I will now look at fractional value
between this. The following is the graph of 0, 1, 2, 2.25, 2.75 and 3. What
happened is that none of the fractional values between 2 and 3 graphed between
2 and 3. They all graphed between 1 and 2.
I am now going to try fractional values larger than 3. The values of 3.75
, 3.875 showed an approach of forming the circle. Then at 3.9 the circle
was formed. The graph of 3.9 looks like a drop and the graph of 3 looks
like an egg.
I will now try some whole number values that are larger than three on the
left side to see what takes place.
When 4 is added to the left side it does not have the circle. I tried the
values of 5 and 10 and the graphs did not have the circles. I presume that
the circle is formed between 3.875 and 3.9. It would be safe to say the
same thing takes place on values being added to the other side. I will check
a few just to be sure.
From the above graph, I have concluded that the graph behaves the same on
both sides. The circle is formed between the values of 3.875 and 3.9.