Write- Up #3


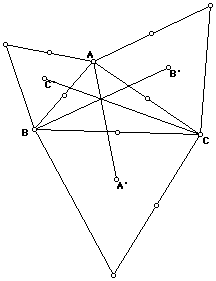
A. The following is a construction of the triangle with the equilateral triangle constructed on is sides. I have also constructed the centroid and the connecting segments.

The segments do have a point that is concurrent.

The point that is concurrent is not the orthocenter, centroid, incenter, or the circumcenter.


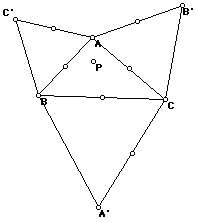
B. The following is the construction of the triangle with the square constructed on each side.

Point p does not appear to be any of the special centers of the triangle

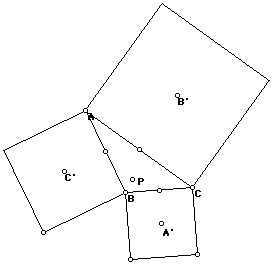
C. The following is a construction with A',B' and C' being the external vertices.

Point p does not appear to be any of the special centers.

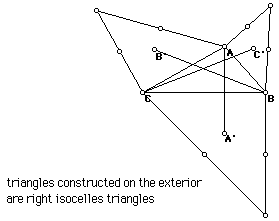
D. The following is the construction of the triangle with special isosceles triangles constructed on each side.

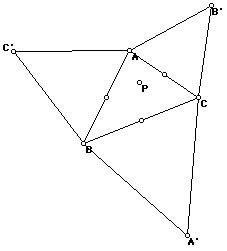
The Point P does not appear to be any of the special centers.


E. The following of the construction with equilateral triangles constructed toward the interior to triangle ABC

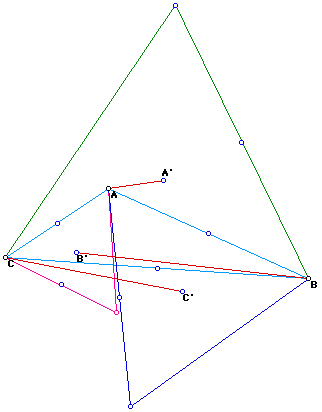
I am not to sure about this construction. The segments AA", BB' and CC' do not over lap. If they do not over lap then they do not have an point of concurrence and then I can not check to see if this point is one of the special centers. What is wrong with this picture?


F. I thought it would be interesting to see what would happen if the external triangles where right isosceles triangles. The problem that I ran into was that the AA' , BB' and CC' did not have a point of concurrence.