---

Inequality in a Triangle

---

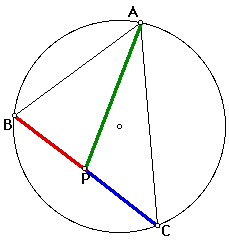
Click here for a problem description

Furthermore we might use GSP to sketch the relationship between the product (PA)(PB)(PC) and the various parameters:

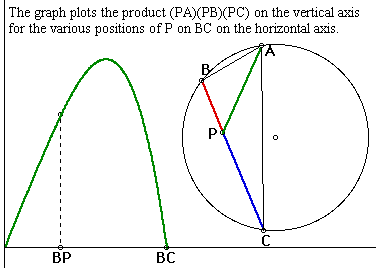
Click the GSP icon for a sketch that illustrates the graph and diagram above.

From playing with the sketch we make the following observations:

• The product seems to be greatest when BC and A are in opposite semicircles,
• When BC and A are as above, the product seems to be greatest when AP contains O (the center of the circle).

Based on these observations and the hint provided in the problem consider the following:

• Construct the diameter AT containing O and P,
• Let OP be x then SP = 1 - x and PT = 1 + x,
• Clearly triangle BPS is similar to triangle CPT, and
• Clearly AP is less than or equal to 1 + x

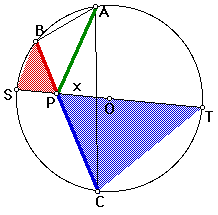
It follows that (BP)(PC) = (1 - x)(1 + x) and hence with equality when AP = 1 + x.

It follows that it remains to maximize (1 + x)(1 + x)(1 - x).

From simple calculus it follows that: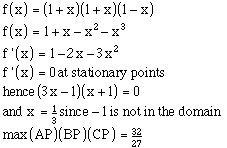

This knowledge provides the basis for a contruction of the family of triangles for whic (AP)(BP)(CP) is a maximum.

Click the GSP icon for a GSP script that draws the family of triangles given a circle.