Running Dogs
Click
here for a problem description
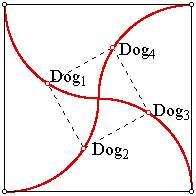
Four dogs
By means of a GSP sketch we can easily see the solution to the problem with
four dogs.
Namely:
- All the dogs meet in the center,
- Each dog follows a quarter circle with radius the side of the square
- The path length for each dog is thus quite clearly:
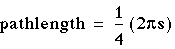
- Each dog crosses each diagonal twice
- The first time is when it starts - the dog is actually on a diagonal
and departs at an angle of 45 degrees to the diagonal.
- The second time it crosses the same diagonal (as the one on which
it started) at 90 degrees and touches the other diagonal (is tangent to)
at the same time.
Click here to watch a GSP animation of
the four dogs running.
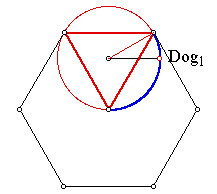
Six Dogs
In this case we consider six dogs starting on the vertices of a regular
hexagon.
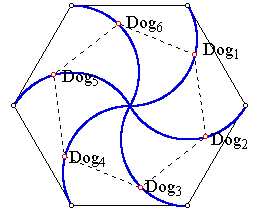
Although the situation is similar to that of the four dogs, they do not
run a quarter circle but rather only a third of a circle, and the radius
of that circle is given by:
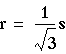
Which follows from the sketch below and the use of the law of cosines
as follows:
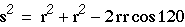
Click here to watch a GSP animation of
the four dogs running.
Return