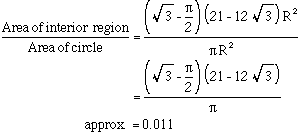
Click here for a problem description
There are two aspects to this problem:
The construction relies on first "seeing" the underlying problem and then on translating that to a construction that has already been dealt with.
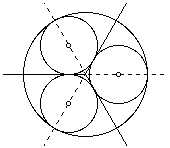
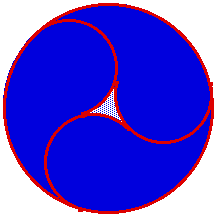
The underlying issue in this problem is to construct three circles interior to the large circle each of them tangent to each other and tangent to the large circle.
Consider only one of these circle, it must be tangent to two radii of the circle (see solid lines) and must meet the large circle where the angle bisector (see dashed lines) of these radii meets the large circle. In our thinking we can really reduce this to constructing a circle through the point where the angle bisector meets the large circle and tangent to ONE of the radii. This final analysis reduces the problem to the construction of a circle tangent to a line and passing throug two (equal) points - a construction dealt with in the Apollonius problem.
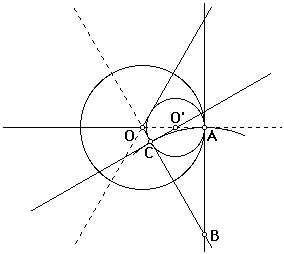
Following the lead from the circle through two points and tangent to a line construction:
Construct a line perpendicular to OA and let it meet the line of interest at B. On OB, mark C so that AB = CB, the center of one of our circles is then found by determining the intersection of the perpendicular to OB through C and the radius OA. The other circles follow in a similar manner.
To determine the area of the interior region it may be helpful to think of that in terms of the triangle O'O''O'''.
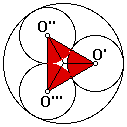
In particular, if we can determine the radius of the interior circles then we will know the sides of the triangle and the area ratio should follow.
To begin, note that triangle OAB is similar to triangle OCO', from which it follows that OA / OC = AB / CO' (ie R / OC = AB / r),
and that: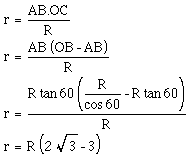 
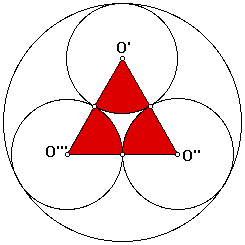The unshaded interior interior of the triangle is derived as follows:
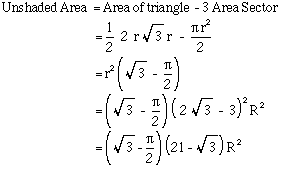
And finally the ratio of the interior space to the whole circle is given by:
