Partitioned Square

---

Click here for a problem description

• there should be a line emerging from each corner of the square to ensure that the right angles are "reduced" to acute angles
• if any line meets a side of the square or another line inside the square then there must be at least one other line meeting at that point

• if lines meet at a point inside the square there should be at least five lines meeting at the point.

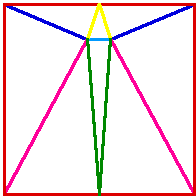
I found the solution above after some time, the question that remains to be asked is whether or not a solution with fewer triangles exists. I claim not!

Justification

• We need at least one line from each vertex of the square, if these lines meet at a point interior to the square we only have four lines meeting at that point and so need another line from that point.

• Since the extra line cannot go to a vertex of the square, it must either go to an edge of the square or to another interior point.
  • If the extra line goes to the edge of the square then we will need another line to emerge from the point of contact with the edge.
    • If this emerging line joins a vertex it will cut at least one of the existing interior lines and in so doing create two more obtuse angles and so require at least two line to emerge from the intersection.

• To avoid such intersection it would seem that a further interior point is desirable.
• If the extra line goes to another interior point we will need a further four lines to meet at the new interior point. If we then arrange the lines as per my solution we avoid intersections which are undesireable and we make the most economical use of all the required lines.

Further questions:

• As I worked on this problem I noticed that in all the solutions that I found there were always an even number of triangles created.
  • Is this always the case?
• What about other shapes: triangles (all different types) etc?