![]()
Where A, i, b and v are respectively the area, the number of interior
points, the number of boundary points and the total number of points of
the polygon.
This rule is known as Pick's Theorem discovered by George Pick in 1899.
While this theorem is relatively easy to "discover" and certainly
not difficult to use, proving it is certainly not trivial.
The following proof of Pick's Theorem by Dale E. Varberg is different
from many of the others and, I think, quite interesting.
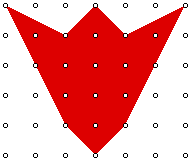
The discussion is restricted to polygons that have boundaries that do not
overlap and vertices that lie on the lattice points of the grid (pegs on
the geoboard).
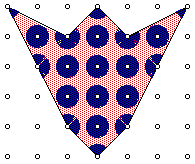
Varberg associates with each lattice point a value (weight) that
is a function of a points "visibility" - the angle with which
the points can "see" into the polygon:
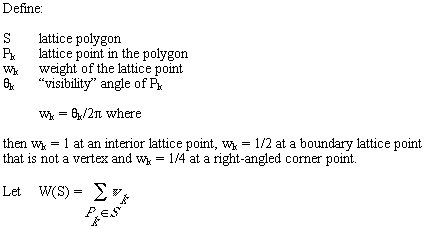
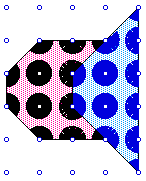
We need to show that W is additive - that is if S = S1 + S2 then W(S)
= W(S1) + W(S2).
This follows from the fact that the visibility angles in S1 and S2 at any
common lattice points add together to give the visibility angles in S at
that point:
Next we want to show that A(S) = W(S) where A(S) is the area of polygon
S. Consider a lattice rectangle with sides parallel to the lattice, a lattice
right angles triangle with legs parallel to the lattice and an arbitrary
lattice triangle which can be surrounded by right-angled lattice triangles
to form a rectangle.
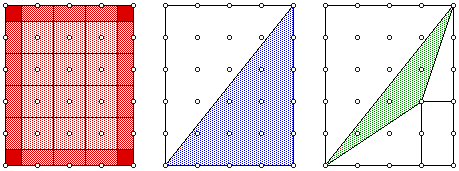
That A(S) = W(S) is obvious for the rectangle, that it is true for the
right-angled triangle follows by dividing the rectangle in two and that
it is true for the arbitrary triangle follows from the remarks that W and
A are additive. Since we can decompose any polygon (of the type we are dealing
with) into lattice triangles we can find A(S) by using the addition of the
triangles.
Interior angle sum of a polygon:
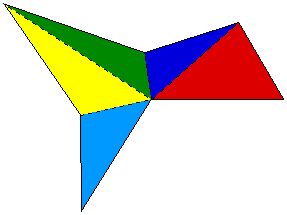
It follows from our ability to divide any polygon with n vertices into
n-2 triangles that the sum of the interior angles of a polygon is (n-2)
pi and Pick's Theorem follows.....
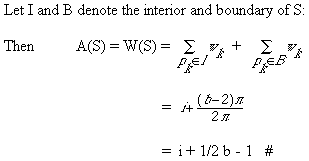
Reference
Varberg, D. E. (1985), Pick's Theorem Revisited. In American Mathematics
Monthly 92 (pp.. 584 - 587); Washington, DC.; Mathematical Association
of America.
"Some years ago, The Northwest Mathematics Conference was held in Eugene, Oregon. To add a bit of local flavor, a forester was included on the program, and those who attended his session were introduced to a variety of nice examples which illustrate the important role that mathematics plays in the forest industry. On of his problems was concerned with the calculation of the area inside a polygonal area drawn to scale from field data obtained for a stand of timber by a timber cruiser. The standard method is to overlay a scale drawing with a transparency on which a square dot pattern is printed. Except for a factor dependent on the relative sizes of the drawing and the square grid, the area inside the polygon is computed by counting all of the dots fully inside the polygon, and then adding half of the number of dots which fall on the bounding edges of the polygon." (De Temple in Grunbaum and Shephard).