

As a wheel travels in a straight line, the locus of any point on its circumference will be a familiar curve known as a cycloid (click the movie button for a movie).
As a wheel rolls on the inside of a circle, points on the circumference of the wheel trace curves known as hypocylcoids whereas when the wheel rolls on the outside of the circle, epicycloids are generated by points on the circumference of the wheel. Finally the curves traced by points on the interior of the wheel are called hypotrochoids and epitrochoids for the wheel rolling on the inside and outside of the circle respectively.
My interest in this paper is to see how we may use Geometer's Sketchpad (GSP) as a tool for exploring the properties of these figures. I claim that students will learn a great deal more about the figures by writing GSP scripts to draw them than they will from either a lecture or a demonstration.
Let me outline what I anticipate a learning experience may entail:
1. Understanding the Problem
GSP has no function whereby you can tell it to "roll the wheel" about a circle. The first task then is to find a manner in which this can be achieved and to do this the student will have to truly understand the problem. That is we need to simulate in some manner a wheel rolling about a circle - since the rolling wheel touches the circle as it rolls, it seems clear that as the wheel completes one revolution it should have touched a fraction of the circle equal to the circumference of the wheel.
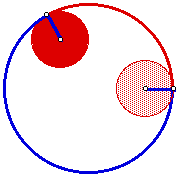
In this figure the rolling wheel has a radius one third of the circle and after one revolution of the wheel it has "touched" one third of the circle. It also important to notice that the radius of the wheel has gone through 360 degrees but the angle between the starting point on the circle and this point of contact is 360/3 = 120 degrees!
2. The Construction
Now that we understand the problem we may begin with the construction.
The key to the construction is the fact that we can both animate two aspects
of a GSP sketch simultaneously and that we can be sure that the point moving
in one animation does so at the same speed as the point in the other animation
(provided that we chose the same setting (quickly/normal/slowly)).
The basis of the construction is as follows:
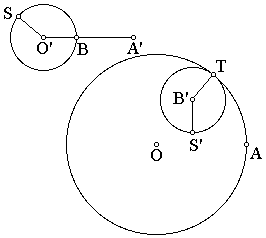
Given a circle center O and radius OA, construct a point T on the circumference of the circle. The wheel is constructed on the radius OT with center B'. The easiest would now be to animate T around circle center O while animating some point (S') around the wheel - GSP does not allow this (since the wheel is a result of the point T and you cannot animate on something that is the result of another animation) and we must introduce a second circle.
Hence the construction: Given OA and the circle (center O passing through A) construct another line O'A' = OA and some point B on the line segment O'A' . The wheel is constructed on radius OT so that O'B = B'T where T is an arbitrary point on the circle. S is an arbitrary point on the image of the wheel (circle center O' and passing through B). Finally we construct S' so that angle BO'S = angle TB'S' and if we now animate T around the circle and S around the image of the wheel we get the desired curve by tracing the point S'.
This construction provides the basis of all the different curves we wish to investigate......
HOWEVER.........
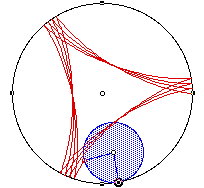
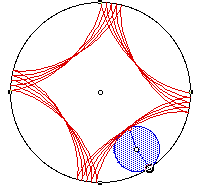
The construction has a small problem with accuracy (which is sadly a function of the software). There are certain properties of these curves that are well known namely: In the case of the hypocylcoids (and epicylcoids) if R/r is the ratio of the radius of the circle to the radius of the wheel and R/r is rational then R will represent the number of cusps while r indicates the number of times the wheel must roll around the circle before the picture is completed (in the figures below R/r = 3, 4 and 2 respectively)
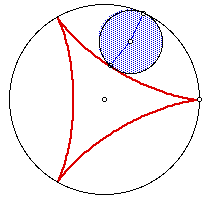
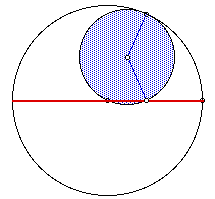
Using our construction sadly results in some inaccuracies... (for discussion of these inaccuracies click here to read some correspondence from the developer)
A different construction
If we return to our original remarks we we recall (and if it was not obvious then - it should be after the first construction) that there is a relationship between the angle through which the wheel has turned and the angle of the circle through which it has moved this can be given by: angle TBS = R/r * angle TOA (and for complete accuracy: angle TBS = - (R/r * angle TOA)).
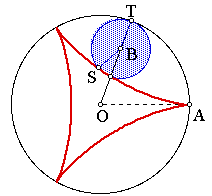
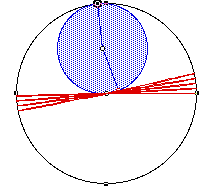
Using this technique clearly overcomes the problem of inaccuracy described earlier. Sadly, however, it introduces another: In the case where R/r is rational and r is not 1 we get (in the case R/r = 3/2):
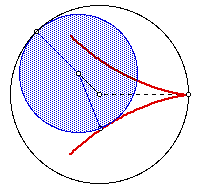
Notice that the locus is incomplete! This is easily understood by considering what is actually happening with our construction:
In the first case (with R/r = 3) as angle TOA approaches 180 degrees - say at 179 degrees angle TBS = - (3 * 179) = - 537 degrees, then as angle TOA passes 180 degrees to say 181 degrees GSP measures the angle as - 179 degrees and TBS = - (3 * - 179) = 537 degrees. Fortunately the angles - (3 * 181) = 573 and 537 are really the same resultant movement of BS and the sketch is not influenced. In the second case (with R/r = 3/2) is we consider the same scenario then as TOA changes from 178 degrees to 182 (= - 178) degrees, TBS changes from - 267 degrees (- (3/2 * 178) = - 267) to (- (3/2 * -178) = 267 degrees and this time 267 degrees and -267 degrees do give the same resultant movement of BS and hence the new problem!
COMPARISON OF CONSTRUCTIONS
Each construction has some advantages and hence some value. The greatest advantage of the second construction is that we can construct the hypocycloid as a locus which enables us to observe the impact of changing R/r without having to animate the curve each time. Click the button for a Quicktime movie that illustrates this remark:
One important observation that you should have made when watching the movie was that the same error that causes the problem when r in R/r is not 1 also causes trouble in this situation - compare the following clip from the movie with the corresponding scene using our other construction (R/r = 7/2 in each case):
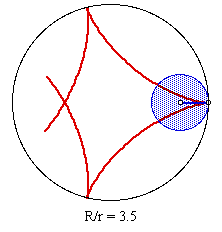
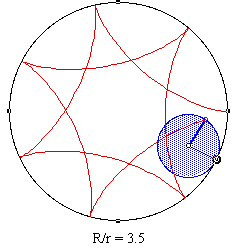
So one is left with the choice - use the first construction despite its inherent flaw (and increase the accuracy by making some adjustments to the actual dimensions of R for each case) OR use the second construction which is technically flawed but gives a more accurate illusion within certain parameters (R/r has r = 1).
3. The Exploration
We are now ready to explore the properties of Cycloids, Hypocycloids, Epicycloids, Hypotrochoids and Epitrochoids
For the purpose of this paper I will only provide illustrations (both figures and movies) and GSP sketches (for the reader to play with).
HYPOCYCLOIDS
To access the GSP sketch used to draw these hypocycloids click the GSP
button: ![]()
R/r = 2: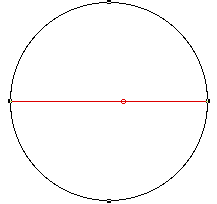
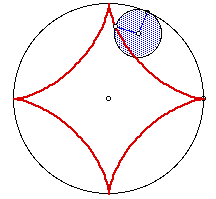
The diameter of the wheel traces the astroid: 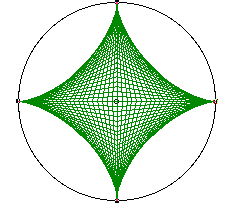
R/r = 4: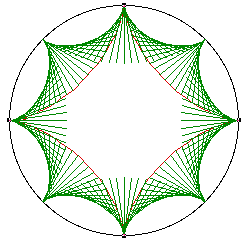 R/r = 4/3
R/r = 4/3 
In the case R/r = 4/3 we get exactly the same hypocycloid as in R/r = 4 (though it is not completely clear in the sketch) but the trace of the diameter of the wheel is quite different!
EPICYCLOIDS
To access the GSP sketch used to draw these epicycloids click the GSP
button: ![]()

R/r = 1 - This epicycloid is called a Cardioid
The Cardioid may also be considered by using some arbitrary points on the circumference of the fixed circle as centers of circles passing through the cusp of the cardioid as in the figure above. We can further think of the cardioid as being created by a circle rolling around the fixed circle and having twice the radius of the fixed circle (consider the hypocycloid construction with R/r = 1/2)
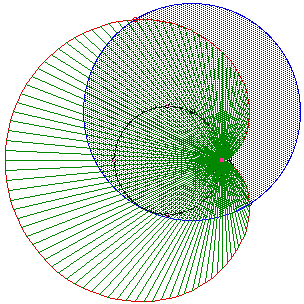
HYPOTROCHOIDS
To access the GSP sketch used to draw these hypotrochoids click the GSP
button: ![]()
R/r = 2, r/f = 2 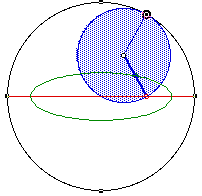 R/r = 3, r/f = 1/2
R/r = 3, r/f = 1/2 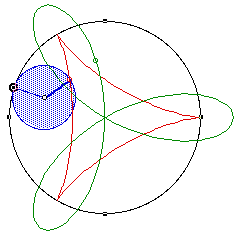
R/r = 8, r/f = 1/4 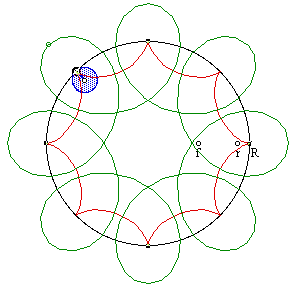
EPITROCHOIDS
To access the GSP sketch used to draw these epitrochoids click the GSP
button: ![]()
R/r = 3/2, r/f = 2 
R/r = 2, r/f = 1/2 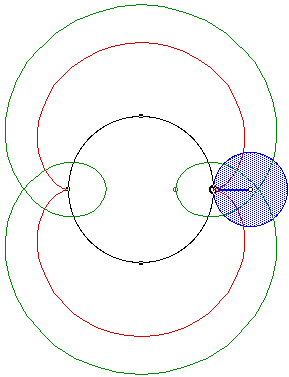
R/r = 6, r/f = 1/4 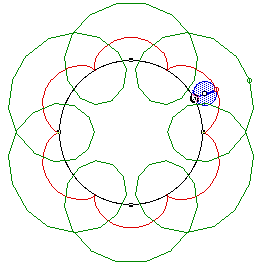
Return to Aarnout's EMT669 page