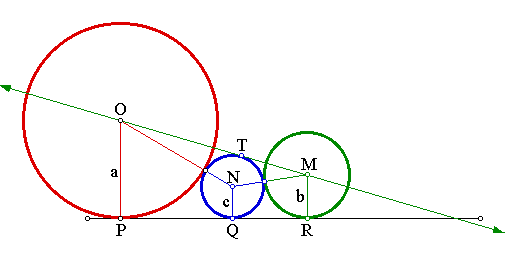
The problem that has come to be known as The Three Circle Problem among those of us in the Winter '97 EMT699 class who have struggled with it for some time, was posed by Dr James Wilson in the EMT 699 course outline (click here to view the problem).
There are two main parts to the problem: 1) demonstrate the construction, and 2) determine the relationship between a, b and c.
After some time a number of us have found constructions but to date nobody has yet been able to determine the relationship. I will begin by sketching the construction that I found and how I came to find it (in part by accident). Dr Wilson offers a GSP sketch that provides a different construction (first discovered by Mary-Beth Searcy). It was our hope that the constructions would be instructive in providing a clue to the second part of the problem - to date no luck.......

The our initial objective is, given lengths a and c construct the line through O (the center of the circle with radius a) passing through T (the point of tangency of the line to the circle with radius c). There are a number of ways of doing this but the underlying idea is illustrated in the sketch below:
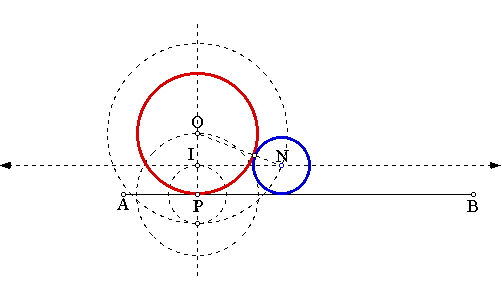
With point P (on AB) as center draw two circles one with radius a and the other with radius c. Through P draw a perpendicular to AB. Let the intersection of the circle with radius a and the perpendicular be O and draw the circle of radius a with O as its center - clearly this circle is tangent to the line AB. Through I, the intersection of the perpendicular line and the circle with radius c, draw a line parallel to AB. With O as center draw a circle of radius a + c, where this circle intersects the line parallel to AB we have the center (N) of the circle with radius c. (NOTE: the construction is described in detail - it is left to the reader to verify that the construction is valid).
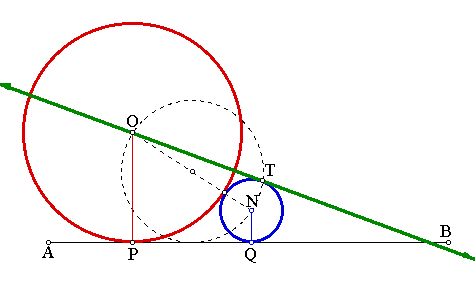
Next we draw the circle with ON as diameter and we call the (upper) intersection with the blue circle T. The line drawn through O and T is tangent to the blue circle. (AGAIN it is left to the reader to verify the validity of this construction).
So with the preliminary work behind us we must now find M - the point on AT that will be the center of the circle with radius b which will be tangent to both the blue circle and the line AB.
Performing a bit of "wishful thinking" we notice that we want a point that is equidistant from N and a line parallel to AB and a distance a "below" AB. We also know that the locus of such a point is a parabola with focus N and directrix - the line described above:
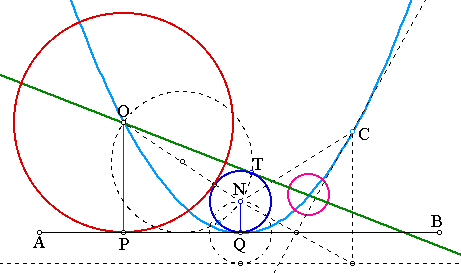
The sketch illustrates the trace of the locus of C the point equidistant from N and the parallel line (we should not be surprised to find that O is also on the locus of C). The pink circle marks the point of interest - the intersection of the parabola and the line AB. This trace, however, gives little if any insight on how to construct the actual point. After some struggling I invoked some knowledge on constructible numbers (a topic, coincidentally, dealt with in my Abstract Algebra class at about that time) to determine that the point was in fact constructible - again such knowledge provides little help with the actual construction.
Sparing the reader the agony of each and every thought I had, I will now demonstrate the construction I "discovered" while playing with GSP in my search for the point of intersection:
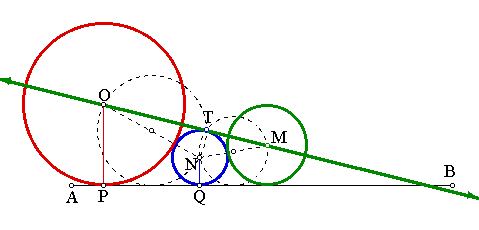
Inspired by the construction technique of point T, it seems obvious that the point M will be the intersection of a circle (that passes through N and T and is tangent to AB) and the line OT.
In other words the problem reduces to:
Given the points N and T on the circle with diameter ON and tangent to AB, construct another circle also passing through the points NT and tangent to AB.
This is what I found:
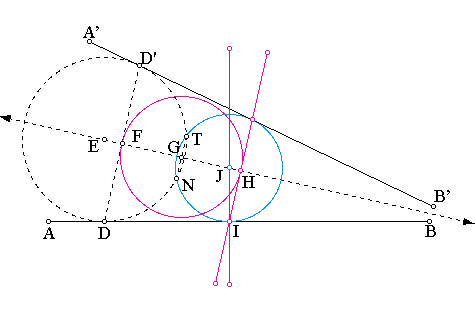
The underlying mechanism.
Let the center of the circle through O and N be E. Join T and N and construct the midpoint G of TN. Draw the line through E and G. Now reflect the point D and the line AB about the line EG to create the tangent A'B' to circle center E with point of contact D'. Join D and D' and name the intersection of line DD' with EG: F. With G as center, draw a circle through F to intersect EG at H. Through H draw a tangent to the circle with center G (ie a line parallel to DD' and passing through H) and let the tangent intersect AB at I. Draw a perpendicular to AB through I and let it cut EG in J. Then J is the center of the circle we are looking for! This results in the construction:
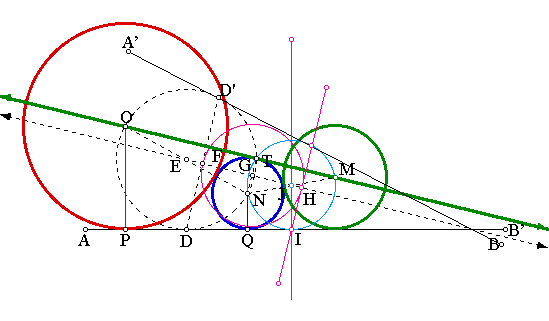
To look at and play with a GSP sketch of this construction click here
Though this is all very nice (and even convincing if we look at the GSP sketch) I am unable to provide a proof that the construction is indeed valid and (probably as a result of this) am no further to providing a relationship between a, b and c.
Frustrated by my lack of progress I visited the library and found at least two constructions which will provide the underlying mechanism. The most interesting was one by Mabel Sykes in her book A Source Book of Problems for Geometry (1912, Allyn and Bacon, Boston, pp 231, 232).
Problem: To construct a circle passing through two given points and tangent to a given line.
Solution: Let AB be the line and C and D the given points. Let CD intersect AB at P. Find the mean proportional between PC and PD. Lay off PQ and PR equal to the mean proportional. Erect perpendiculars to AB at Q and R. Draw the perpendicular bisector of DC, meeting the perpendiculars at O and O'. Prove that O and O' are the required circles.
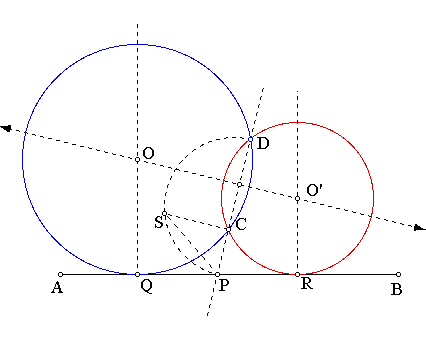
A beautiful construction - and what is more it provides support for the notion that FG anf GH should be equal in my construction.
WHERE TO NOW
At this stage I am, as indicated still far from a solution to the problem both in terms of proving the validity of the construction and in terms of finding the relationship between a, b and c. What I would like to do is illustrate a few avenues that I am currently exploring:
SIMILAR TRIANGLES
There are an abundance of similar triangles at play in the sketch and I had hoped that these may provide an insight into the elusive relationship:
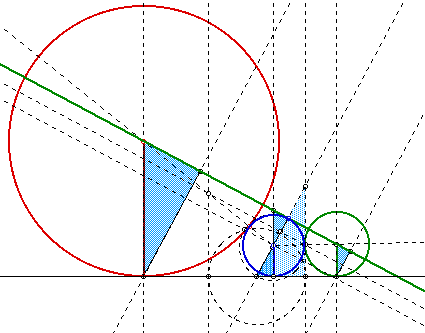
GRAPHICAL RELATIONSHIP BETWEEN a, b AND c
Another avenue of investigation was to use GSP to draw the relationship between a and b for different values of c, the result is not surprising (click on the movie button for a movie that animates the situation or on the GSP button for the GSP sketch):

Using the GSP sketch above I gathered some data and used both Ti- 81 and Mathematica to try and find a relationship between a, b and c using regression techniques but this was not a very successful venture.
A DIFFERENT CONSTRUCTION
After the many hours playing with the problem and inspired by the Mabel Sykes construction I realise that it is enough to have the dimensions of c to be able to make the general construction. For a GSP script that draws the sketch click here.
CONCLUSION
This problem is far from resolved and while I will continue to work at it I would be delighted at suggestions on how to proceed from anybody who might read this discussion (email address on the main page).