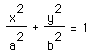Orbits
A lesson series by Aarnout Brombacher
(EMT 705 - Summer 1997)
Background
I have enjoyed a long standing fascination with space flight and while
too young to remember the moon landings, I remember clear as anything the
day the first space shuttle landed back on earth. My family did not have
television yet (at that time a relatively new commodity in South Africa)
and I had to make special plans to visit the home of friends to watch the
landing - a marvel of modern science! If you just think about what was achieved
during the landing (and all other aspects of the flight) you cannot but
be impressed. The space shuttle is for all intents and purposes a glider
which had to enter the atmosphere at a precise moment so that it would touch
down on a runway that could not be seen from space - and at the heart of
that and many of the other maneuvers was mathematics. More recently while
studying at the University of Georgia I managed to organize a Kennedy Space
Center launch pass for the launch of Columbia on mission STS94 and the dream
of watching a shuttle launch came true.
The recent landing of the Mars pathfinder (4 July 1997) was another historic
moment in space travel. At one of the press conferences televised on the
day, Pieter Kallemeyn, the navigation team leader, described the process
by which the navigation team had guided the Pathfinder to Mars, and how
they were (just minutes before landing) certain that the Pathfinder would
land in a "footprint" elliptical in shape some 100 km long and
20 km. wide. It astounded me to think that the Pathfinder had traveled some
300 million kilometers and that the navigation team could be so close in
its predictions of a landing sight - just think of what they had achieved:
an essentially unpowered vehicle (Pathfinder) had left a spinning object
traveling on some orbit in space (Earth), had traveled along its own orbit
(determined entirely by the forces of the solar system) for more than seven
months (with only three tiny corrections to this orbit as it flew) and finally
it would land on another spinning object traveling on its own orbit (Mars).
With all these variables the navigation team were confident of a landing
site with dimensions that seem insignificant in terms of the dimensions
of the whole venture!
There was an amusing incident during the press conference described above.
One of the journalists, reacting to Pieter Kallemeyn's remarks about the
dimensions of the landing site and other scientists' remarks about entry
angle and time of landing, asked a question to the effect of: "Why
do we have to deal with all this inaccuracy?" I was amused by these
remarks for they reflected a complete lack of understanding for the very
high degree of accuracy that had been achieved by the project team,
in terms of the variables involved I could only imagine that the percentage
error reflected in the scientists predictions that morning were of an entirely
negligible order. Let us not forget though that such precision was essential
for the success of the mission!
Pieter Kallemeyn's remarks inspired me to write this lesson series on
orbits in the hope that students might both appreciate an application of
the mathematics they study and that they may be impressed by the complexity
of what is achieved when a space shuttle rendezvous with a satellite, or
the Pathfinder actually lands on Mars, or even (and quite critically) when
a space shuttle does not rendezvous with flying debris and satellites in
orbit around the earth!
Writing this lesson series is a double challenge, to write it I have
had to learn a great deal about space flight to be able to write units that
are realistic and authentic, the second challenge is to write the lesson
series for use with the internet as I would like to both explore this medium
as an alternative to a traditional printed form and because I would like
to both incorporate technology and the internet in the lesson series.
Lesson outline
Characterization of the application
Conic sections and in particular ellipses are integral to space flight.
The movement of space vehicles in space, the planets and all other elements
of the solar system is governed by a number of forces best described by
seven laws, namely Kepler's laws (3), Newton's laws (3) and the law of universal
gravitation (often attributed to Newton). Our observations tell us and the
laws are able to demonstrate that all bodies in the solar system move along
paths that are conic sections.
Another important observation about space flight is that space vehicles,
like other objects in the solar system, are not powered - that is their
motion is determined solely by their inherent features (mass, initial velocity,
initial position etc.) and the laws mentioned. The important implication
of this is that unlike flying an airplane or driving a car, space vehicles
cannot simply turn corners or change direction, their travels are guided
by forces greater than the navigators who plan their routes! The role of
the mission navigator is to understand the forces that are involved and
to harness these to guide space vehicles on their mission.
One of the important aspects of the navigator's knowledge is an understanding
of conics. In this lesson series we will be exploring the properties of
conic sections - more accurately the properties of ellipses as a subset
of the conics and will be trying to understand the role of such conics in
space travel.
Instructional Objectives
On completing this lesson series students should:
- recognize that ellipses are a subset of the conics,
- be familiar with two different definitions for ellipses,
- be able use these definitions to find equations for ellipses,
- understand the derivation of both Cartesian and parametric representations
of ellipses,
- be able to use orbital elements (apogee and perigee) to determine the
parameters needed to use the equations,
- be able to use their graphing utilities to plot ellipses in both Cartesian
and polar form,
- understand that the discussions of this lesson series with respect
to space travel are a much simplified model of reality,
- realize that mathematical models are at the heart of space travel -
that is that mission scientists are unable to deal with all the variables
involved in missions and use models which they modify as they gather data.
- recognize the power of mathematical modeling in the sense that they
will have observed a complex situation being reduced to some simplest case
and then built up one variable at a time,
- be able to describe some fundamental features of space flight and planetary
motion in terms of mathematical relationships.
Incorporation of the Lesson Series in the Curriculum
There are two ways in which I anticipate teachers incorporating this
lesson series in the curriculum:
- The lesson series can form the foundation for the teaching of conic
sections, in this case the lesson series (as it stands at the moment) will
need some additions to deal with hyperbola (Comets) and parabola.
OR
- The lesson series can be incorporated as an enrichment activity with
a lesson series on conics - I must confess that I would regard this as
second prize.
I hope to develop the lesson series some more in the months to come and
hope to use it as the basis for the teaching of conic sections when I return
to teaching in January.
Prerequisite Knowledge
Students participating in this lesson series should be familiar with
the following:
- basic algebra - enough to be able to manipulate some simple expressions
and equations and to be able to solve simple equations,
- elementary trigonometry of right angled triangles (used in deriving
the polar form of the equation for an ellipse),
- proficiency in using graphing calculators (or some other graphing utilities)
and some geometry program (e.g. GSP) - of course proficiency is not essential
as proficiency will also be developed by the use of these technologies
during this lesson series, and
- some familiarity with the fundamental equation for ellipses -
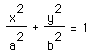
NOTE: by my way of thinking none of these topics are completely prerequisite
as the need for them in the lesson series could be the motivation for learning
those topics. To, however, use the lesson series as written would require
the knowledge outlined above.
Materials
The lesson series assumes that students have access to:
- The internet to read the lessons, take advantage of the numerous links
provided and gather the data required for the completion of many of the
tasks.
- QuickTime: the materials assume
that the webb browser students are using has the QuickTime plug in required
to look at some of the movies built into the lesson and some of the movies
that the lesson links to. To download QuickTime free of charge click here.
- GSP: the materials assume that
students have GSP both configured as a helper for their browser and as
a program to work with. To download a preview version of GSP click here.
Furthermore, while hardly critical to the success of the lesson, there
is a fabulous video that would help teachers as they manage the lesson
series: Space Flight: The Application of Orbital
Mechanics (NASA Core). For details of how to order the video
and the book Space Mathematics - A Resource for Secondary
School Teachers (NASA) that comes with the video, click
here.
Click here for a break down of the video
in terms of content.
Lesson Plans
The lesson plans are presented in two parts; teacher notes to lesson
units and the student notes. The way things have worked out the student
notes are more than a series of instructions to students and could be regarded
as a self contained series of lessons for students to work through by themselves.
For the full benefit of the lesson series to be realized, the teacher plays
the critical role of setting the scene, directly teaching some of the topics
and helping students as they work through the tasks many of which are definitely
non-trivial.

Teacher Notes to Lesson Units
Click the orbit icon to go to the teacher notes for the lesson units.
 Student
Notes
Student
Notes
Click the orbit icon to go to the student units of the lesson sequence.
NOTE if teachers wanted students to use this lesson series without access
to the teacher materials then they would simply get them started by having
them open the following URL with their webb browser:
http://jwilson.coe.uga.edu/EMT668/emt668.student.folders/BrombacherAarnout/Orbitslesson/studentopening.html
Sadly this address is a little long but the students could make a bookmark.
Assessment
As already indicated in the Teacher notes to the lesson units, unit six
is regarded both as a capstone unit and as a substantial component of the
assessment for this unit. I would suggest that the following would comprise
the assessment for this lesson series:
- Portfolio: Each student should hand in
a portfolio on completing the unit which comprises the following:
- A cover letter that outlines the essence of the problem that has been
dealt with during this lesson series, a discussion of the mathematics that
the student has learned during the series and some remarks about how they
have enjoyed (or not) the series.
- A selection of problems completed during the series which best illustrate
what the student has learned and which support remarks made in the covering
letter.
- An outline of their finding from their extension activity.
- The use of graphs (printed or rough sketches) should be encouraged
throughout.
- Extension Activity: Each student should
hand in a summary of what they have found during their extension activity,
this should be no more that 10 pages but at least 5. The following should
be important criteria by which the assignment is assessed
- Mathematical accuracy - all remarks should be well substantiated and
evidence for conclusions should be provided.
- The assignment should take the form of a exposition, in that it should
be trying to teach something. An incentive might be that teachers will
build links from this activity to exemplary assignments as hints for future
students.
- At least one suggestion should be made for an extension to the work
done by the student.
- Test: Depending on the style of the teacher
a test may be administered during a class period, it could include:
- The graphing of an ellipse using both the Cartesian equation and polar
form.
- The graphing of a pair of orbits and their Hohmann transfer orbit built
by the student.
- The derivation of the polar form of the equation (either completely
or simply some parts of it).
- Locus definitions for ellipses.
Resources and References
References
Edwards, C. H. and Penney, D. E. , (1985). Calculus and Analytic Geometry.
New Jersey, Prentice Hall.
Jet Propulsion Laboratories, (1995). Basics of Space Flight Learners'
Workbook. California, JPL.
National Aeronautics and Space Administration, (1985). Space Mathematics
- A Resource for Secondary School Teachers. Washington, NASA.
National Council of Teachers of Mathematics, (1997). Mission Mathematics
- Linking Aerospace and the NCTM Standards (9 - 12). Reston, NCTM.
Resources
Internet links:
Video
- NASA Central Operation of Resources for Educators (CORE). Space
Flight: The Application of Orbital Mechanics.
Return to Aarnout's
page