An investigation of
for n = 2, 3, 4, ... . Eventually we hope that students will recognize
distinct patterns for both the even and odd exponents.
Once students are familiar with quadratic equations in one variable, we
may ask them to predict what will happen in a quadratic equation in two
variables.
For example,
for various values of n. Students may choose to use a graphing calculator
or any relational graphing tool. We chose Algebra Xpresser to create our
graphs.
As demonstrated below, graphing both even and odd values of n on the same
axes may make interpretation more difficult.
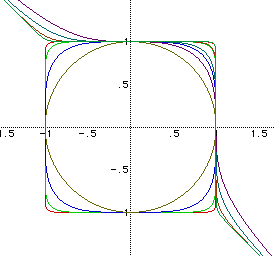
Thus, we separated our exploration into even and odd values of n.
(You may want to suggest this to your students.) The following is a graph
for n = 2, 4, 10, and 24. We have found that if students view subsequent
graphs with the previous graphs still visible, they may find it easier to
follow the trend of the equation as n varies.
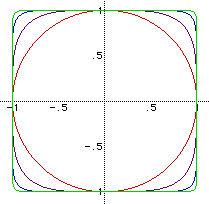
As students view this graph, they may notice that when n=2 the graph
is a unit circle. As n grows larger, the circle seems to approach a unit
square. However, this graph is misleading because it appears that for n=24
there are vertical line segments at x = 1,-1 as well as horizontal line
segments at y = 1, -1. Yet, we know that this is impossible for this equation.
When x = -1, the only possible y-value is 0. Similarly, at x = 1, y=0. Obviously,
for these equations, -1 <= x <= 1 and -1 <= y <= 1, due to the
nature of the even exponents . Thus as n increases, the vertical line is
approached from inside the unit square, but is never reached.
The following is a graph for n = 3, 5, 11, and 25.
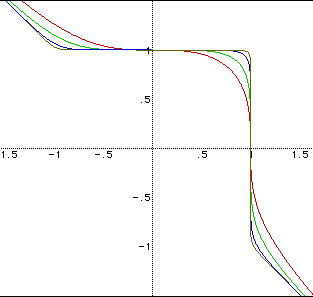
Again the students should graph each equation consecutively on the
same axes, in order to recognize the trend. For n=3 (red curve), the graph
crosses the y-axis at y=1 and then intersects the x-axis at x=1. For n=25
(tan curve), the graph appears to include vertical and horizontal line segments
at these points. But with further investigation we find that y=1 only when
x=0 and x=1 only when y=0. Thus, the graphs must continue to cross at these
points, approaching vertical and horizontal line segments, but never reaching
them. For these graphs, the area of interest remains within |x| < 2 ,
|y| < 2. But we can see that as x increases, the y must decrease and
vice versa, for all odd values of n.
As an extension, students may look at a similar equation in three dimensions
such as,
Another area of exploration might be to include an x-y term in the
two dimensional case such as,
This investigation demonstrates the relative ease with which students
can investigate "new" equations, and helps students see the need
to test their interpretations of the graphs. For example, in this investigation
we found the apparent horizontal and vertical lines to be potentially misleading
to students unfamiliar with these equations. This is not to say that students
should not be using technology, but rather that we as teachers need to encourage
students to consider the validity of their results and conclusions regardless
of the method used, pencil and paper, calculator, or computer.
Furthermore, if the students look more closely at the graphs, they may get
a better feel for mathematical concepts, that may not be included in the
traditional curriculum at that stage. In particular the graphs of the even
exponents (see above) seem to approach the shape of a square, but as stated
earlier in fact never reaches a square. This is a graphical representation
of limit and could be used as an introduction to that topic.
Thus technology is a good resource for introducing or exploring new topics,
testing conjectures, and motivating extensions further into the given topic
or into a related topic.