An Investigation of
Points of Concurrency
by
Helene Chidsey
and
Lou Ann Lovin
In the following investigation we explore points of concurrency and share
some interesting observations we noticed along the way.
I
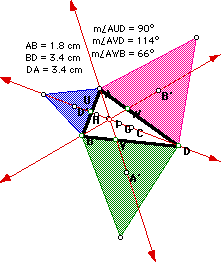
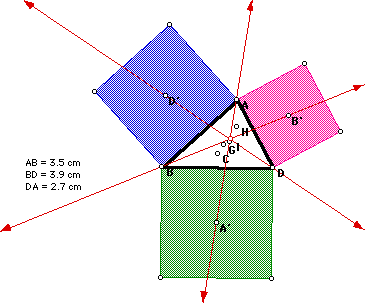
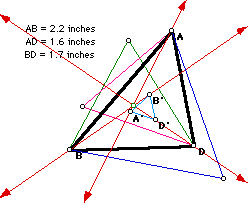
On each side of an arbitrary triangle ABD, we
constructed external equilateral triangles using the length of the corresponding
side of triangle ABD. We then located the centroid of each exterior equilateral
triangle (labled A', B', D', where A' is opposite vertex A, B' is opposite
vertex B, and D' is opposite vertex D). Notice that the lines AA', BB',
and DD' intersect at one point.
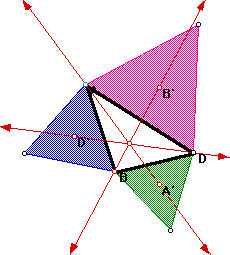
First, we checked the most commonly known centers, the orthocenter
(H), the centroid (G), the incenter (I), and the circumcenter (C) of triangle
ABD. However, we noticed that for an arbitrary triangle ABD the point of
concurrency was not any of those centers. Using GSP we played with triangle
ABD to determine what happens to these centers and the point of concurrency
as the triangle changes shape. Click here for a GSP
link.
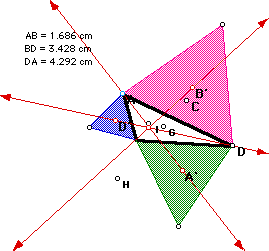
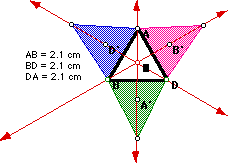
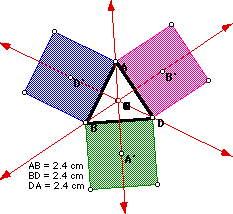
Notice when triangle ABD is an equilateral, that G, H, C, I and the
"new" point are all concurrent.
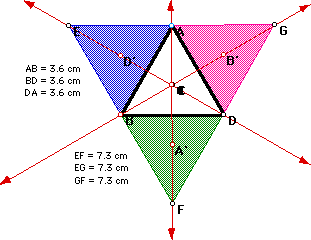
In the above picture we also see that the large triangle EFG is an equilateral
triangle only when triangle ABD is an equilateral triangle. Let x = the
side length of triangle ABD. Since the external equilateral triangles were
constructed using the length of the corresponding side of triangle ABD,
each side of triangle EFG has length 2x.
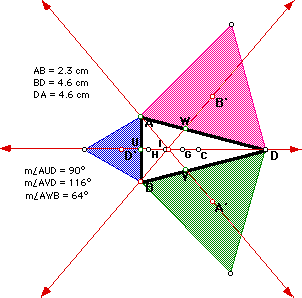
When the triangle ABD is isosceles, all the points of interest lie on
the perpendicular bisector of the base. Try manipulting ABD so that one
of the other sides is the base and see if this is still true.
GSP link.
The reader is encouraged to visit the Geometer's Sketch Pad link to manipulate
triangle ABD and watch the movement of the different centers as well as
the point of concurrency. You will notice that the incenter (I) follows
the point of concurrency closely, but only rests on top of it when ABD is
equilateral. GSP link.
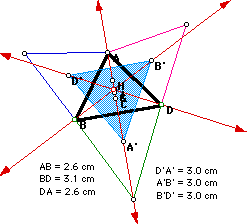
We then connected the centroids A', B', and D' to form a triangle, and
found that A'B'D' is always an equilateral triangle, regardless of the shape
of triangle ABD. We also checked to see if the point of concurrency is one
of the centers (C,G,I, or H) of triangle A'B'D', but found that it is not.
Again the reader is given the opportunity to manipulate this figure. GSP
link.
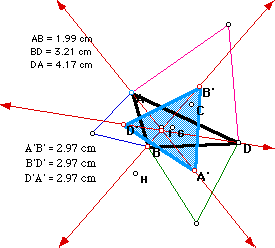
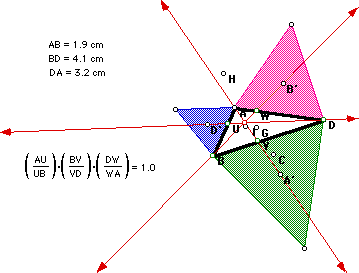
Finally, we looked at the ratios of the sides where the lines AA',
BB', and DD' cut the triangle ABD, and discovered that regardless of the
form of triangle ABD, the product of the ratios is one. Connect to GSP to
convince yourself! GSP link.
(Click here for a brief proof.)
II
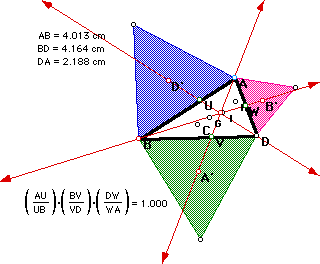
Part II of this investigation is similar to
part I, but instead of external equilateral triangles, we constructed external
isosceles triangles with height equal to the length of the corresponding
side of triangle ABD. We then located the centroid of each isosceles triangle
(labled A', B', D', where A' is opposite vertex A, B' is opposite vertex
B, and D' is opposite vertex D). Again the lines AA', BB', and DD' intersect
at one point, and this point of concurrency is not the orthocenter, centroid,
incenter, or circumcenter of triangle ABD.
As in part I, when triangle ABD is an equilateral, all of the points
are concurrent and when ABD is isosceles, they all lie on the perpendicular
bisector of the base. GSP link.
The large outer triangle, is almost isosceles when triangle ABD is an
equilateral triangle. Notice, we say almost isosceles, because the sides
of the smaller triangles do not quite lie on the line that would connect
the vertices of the larger triangle.
The triangle formed by connecting the centroids A', B', and D' is equilateral
when triangle ABD is equilateral, and when triiangle ABD is isosceles.
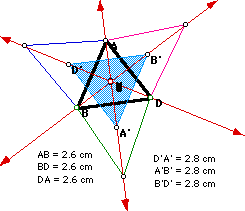
Convince yourself that this happens; go play! GSP
Link.
Once again, we checked to see if the point of concurrency of AA', BB',
and DD' is perhaps one of the afore mentioned centers, i.e. C, G, I, or
H, of triangle A'B'D'. Check for yourselves. Go to GSP and see if the points
match up! GSP link.
Consider again the product of the ratios of the sides where lines AA',
BB', and DD' cut the triangle ABD. Interestingly enough, the product is
again one, regardless of the form of triangle ABD. Check our claim in GSP
! (See part I for a brief proof.)
III
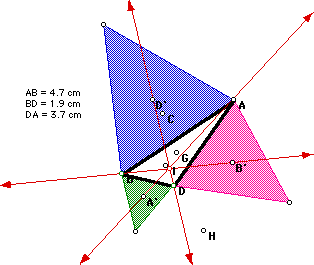
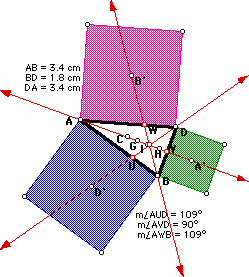
In part III we constructed external squares
on the sides of triangle ABD, and located the centers of the squares (labled
A', B', D', where A' is opposite vertex A, B' is opposite vertex B, and
D' is opposite vertex D). Again, the lines through AA', BB', and DD' have
a point of concurrency, which is not the orthocenter, incenter, circomcenter
or centroid of ABD. Feel free to investigate! GSP link.
As in parts I and II, we found that when triangle ABD is an equilateral
triangle, all the centers are concurrent, whereas when the triangle is isosceles,
all the centers lie on the perpendicular bisector of its base. GSP
link.
We then connected the centers of the squares, forming trinagle A'B'D',
and found that the point of concurrency was not one of the centers I, G,
H, or C of A'B'D'. Connect to GSP to check that triangle A'B'D' is an equilateral,
when ABD is an equilateral, and isosceles when ABD is isosceles! GSP
link.
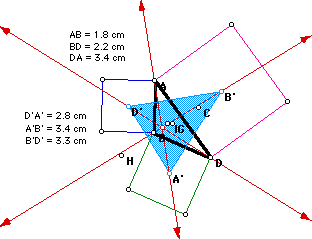
Lastly we looked at the ratios of the sides where these lines AA',
BB', and DD' cut the triangle ABD. Again the product of the ratios is one.
(See part I for a brief proof.) GSP link.
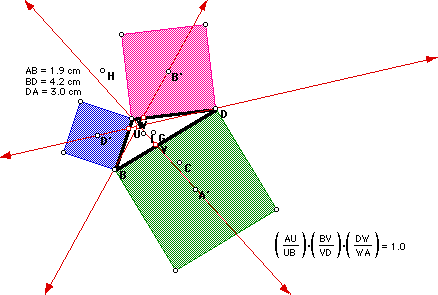
IV
In part IV, we constructed external equilateral
triangles, as in part I, however, this time we did not find the centroids
of the external triangles. Instead A', B', and D' are the external vertices
of the externally constructed equilateral triangles (where A' is opposite
vertex A, B' is opposite vertex B, and D' is opposite vertex D). Again the
lines AA', BB', and DD' are concurrent, but again this point is not the
orthocenter, incenter, circumcenter, or centroid.
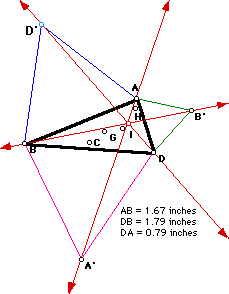
As in parts I, II, and III when triangle ABD is equilateral, all
the centers are concurrent, and when ABD is isosceles, the centers lie on
the perpendicular bisector of the base. To explore these particular forms
of ABD connect to GSP!
We then connected the external vertices of the external equilateral
triangles and found that the point of concurrency of AA', BB', and DD' is
not the orthocenter, circumcenter, centroid, or incenter of triangle A'B'D'.
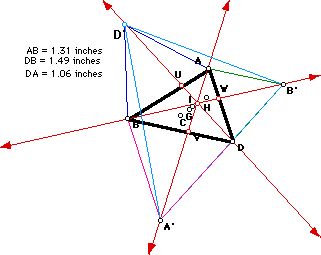
To see that A'B'D' is equilateral when ABD is equilateral, and isosceles
when ABD is isosceles connect to GSP.
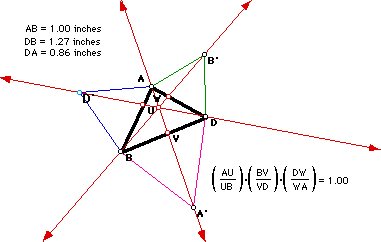
We then looked at the ratios of the sides where these lines AA', BB',
and DD' cut triangle ABD, and again the product of the ratios is one. If
you still do not believe us, check it out, or
see the proof in part I!
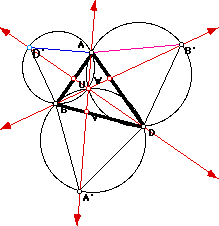
Next we constructed circumcircles around the external triangles,
and found the point of concurrency for this configuration! This point is
the intersection of the circumcircles of the exterior equilateral triangles,
which is the Fermat point!!!! To see that these circles intersect regardless
of the form of ABD connect to GSP.
V
We leave part V mostly to the reader. We constructed
equilateral triangles toward the interior of triangle ABD, found the centroids
of those triangles labeling them A', B', and D' respectively. This configuration
has all of the same properties as the construction in part I. In fact, go
to our GSP file and notice that triangle turned
"inside out" is the same as the triangle in part I.
We can make a few generalizations based on this
investigation. From part IV it is clear that lines passing through the corresponding
vertices of ABD and the exterior triangles have a point of concurrency,
namely the Fermat point. It should also have become clear that any regular
polygon constructed on the exterior of a triangle with lines passing through
the respective centroids and the vertices A,B, and D of the original triangle
will have a point of concurrency which is not the incenter, circumcenter,
orthocenter, or centroid. Additionally, the product of the ratios of the
line segments formed by those lines cutting ABD is always one.
back to Helene's
Webpage.






















