Conic Sections

by

Angie Head and Emily Willis

Introduction

Conic sections were discovered by Menaechums, a Greek mathematician, in the third or fourth century BC. He dicovered conics while he was trying to solve the problem of doubling a cube. He was the first to show that the conics could be obtained by cutting a cone with a plane. Much of our knowledge about the early history of conics is due to the works of Apollonius. Apollonius, another Greek mathematician, wrote an eight book collection titled Conic Sections in the second century BC. Apollonius supplied the names ellipse, parabola, and hyperbola to describe the shapes of the conics. The early Greeks were primarily concerned with the geometrical properties of conics. It wasn't until the 16th and 17th centuries that people began to use conics to solve pratical problems. Mathematicians and astronomers such as Copernicus, Galileo, Johann Kepler, and Issac Newton used conics to describe the motions of objects on the earth and in space.

Three ways to introduce conic sections

The first way to introduce conic sections is to define them as Menaechums defined them. Conics are the intersections obtained when a cone is cut by a plane.

The second way is to define conics algebraically in terms of the general second-degree equation

The third way is to define the conics as a locus of points satisfying a certain geometric property. This is the approach that we are going to take.

Parabola

A parabola is the set of all points (x,y) that are equidistant from a fixed line, the directrix, and a fixed point, the focus, not on the line.

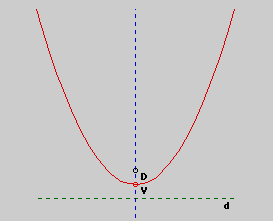
In the above diagram, V is the vertex of the parabola, D is the focus, and d is the directrix.

The standard equations

The standard equations of a parabola with vertex (h,k) is

if the parabola is along the vertical axis and

if the parabola is along the horizontal axis.

Paper-folding investigations for the parabola

In this investigation, we will determine the type of curve that results from the following constructions.

Materials needed
wax paper
pencil

Instructions
Draw a line l and a point P not on the line. Fold and crease the paper so a point O on the line coincides with P. Repeat this process until you can determine the shape of the curve that is being formed. Be sure to use different points O on the line. Repeat this invesitigation using different point P. How does the distance from P and l affect the resulting curve?


Investigations for Parabolas Using Algebra Expresser and GSP:

Here we would like the students to investigate parabolas using Algebra Expresser and GSP. In Algebra Expresser the students would look at the standard equation of a parabola. The students would then investigate this equation by varying values for h,k, and a. What happens to the parabola as each value is increased or decreased? What happens if a is negative?

For GSP construction the students would begin by constructing an arbitrary line and an arbitrary point. Now, create a point on the line by choosing the Point on Object command from the Constuct menu. Your challenge is to construct the line that represented the crease in your paper . You might want to look back at your paper folding exercise to get a clue as to how you would do this. After you construct this line, select it and choose the Trace Locus command from the Display menu. As you drag point D back and forth along line j you'll trace the outline of your curve.

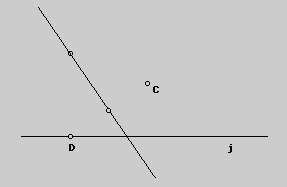
Experiment with different locations of point D to see the change in appearance of the curve you trace. Describe your findings. Also describe what happens to the curve when you drag and rotate line j.

Applications for Parabolas:

A cable of a parabolic suspension bridge
The path of a projectile
The path of searchlights, telescopes, and radar detectors
Ellipse:

An ellipse is the set of all points (x,y) the sum of whose distances from two distinct fixed points (foci) is constant.

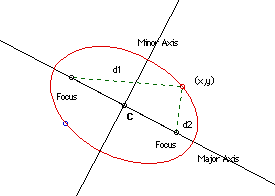
The vertices are located at the intersection of the line through the foci and the ellipse. The segment joining the two vertices is called the major axis and its midpoint is the center of the ellipse labeled C is the above sketch. The chord perpendicular to the major axis and passing through the center is called the minor axis.

The Standard Equation of an Ellipse:

The standard form of the equation of an ellipse, with center (h,k) and major and minor axes of lengths 2a and 2b, where a>b, is



Hands on investigations of the ellipse

Ellipse - paper folding

Materials needed
wax paper
compass

Instructions

1. Draw a circle on the wax paper
2. Label the center of the circle C
3. Pick a point F inside the circle
4. Select a point A on the circle and fold the paper so that point A coincides with point F
5. Make a sharp crease in the paper to keep track of this fold
6. Continue this process by picking other points on the circle until you can identify the type of curve being produced.
7. Discuss the results with your classmates. What are the similarities and differences between the shapes you and your classmates have made?

Applications for Ellipse:

The path of planets around the sun
The path of comets
The orbit of satellites
Optics
Hyperbola

A hyperbola is the set of all points (x,y) the difference of whose distances from two distinct fixed points (foci) is constant.

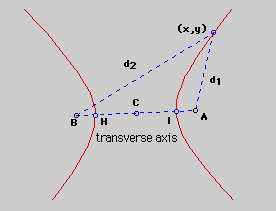
In the above figure, A and B are the foci, C is the center of the hyperbola, H and I are the vertices and d(1) and d(2) are the distances to the foci from (x,y).

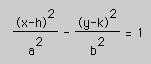
The standard equation of a hyperbola

The standard equation of a hyperbola with center at (h,k) is

if the transverse axis is horizontal and

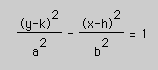
if the transverse axis is vertical.

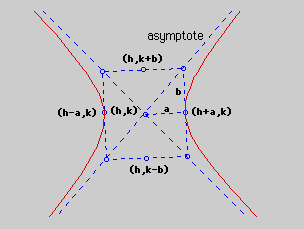
Equations for the asymptotes of a hyperbola

If the transverse axis is horizontal, the equation for the asymptotes are

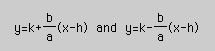
and if the transverse axis is vertical, the equation for the asymptotes are

Hyperbola:

The line through the two foci intersects a hyperbola at two points. These two points are called the vertices. The segment connecting the two vertices is called the transverse axis, and the midpoint of this segment is the center of the hyperbola.
Hands on investigations of the hyperbola

In this exploration, we will use the definition of a hyperbola to draw the rest of the follwng hyperbola.

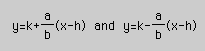
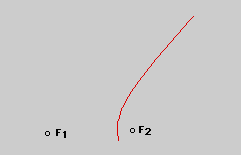
Materials needed
ruler

Steps

1. Choose a point A on the incomplete hyperbola shown above. Measure the distance AF1 and AF2.
2. There is exactly one more point B on the hyperbola such that AF1=BF1 and AF2=BF2. Draw and label this point in the figure above.
3. There is at least one more point C on the hyperbola such that AF1=CF2 and AF2=CF1. Find all points meeting these conditions and draw and label them.
4. Use the above information and draw the rest of the hyperbola.
5. Compare with your classmates.

Investigations for Ellipses and Hyperbolas Using Algebra Expresser:

In using Algebra Expresser the students would use the standard equation for the hyperbola and ellipse to investigate different scenarios. The student would be asked to vary the values of h, k, a, and b. What happens if a is larger than b? If b is larger than a?
Construting an ellipse on GSP

Steps
1. Construct circle C
2. Construct point F inside C
3. Construct point A on C
4. Your challenge is to construct the line that represents the crease when point A is folded onto point F.
5. After you have constucted this line, select it and choose Trace Line from the display menu. Now drag A along the circle. What curve appears?
6. Now construct an animation button so that A will automatically travel around circle C. To do this, select point A and the circle. From the edit menu, choose action, animation, and animate. An animation button will appear on your sketch. Double click the button to begin the animation. You will get something similar to the following:

Once you are finish answer the following questions.
1. What happens when you move point F closer to the edge, closer to the center, on the circle, and outside the circle?

Applications for Hyperbolas:

LORAN -- Long Distance Radio Navigation
The path of comets
Telescopic lenses
Angie's Home Page