Sequences:
Arithmetic and Geometric

by

Angie Head


In this essay, I am going to investigate different arithmetic and geometric sequences using Excel. Students are introduced to various arithmetic and geometric sequences in high school. This essay is designed to help students develop a better understanding of these sequences by investigating and interpreting various kinds of graphs.

Before I begin my investigations of sequences, I want to give a few definitions so that we will all be starting from the same point. A sequence is defined as a function, an, having a domain the set of natural numbers and the elements that are in the range of the sequence are called the terms, a1, a2, a3,...., of the sequence. All the elements of a sequence are ordered. There are two kinds of sequences, finite and infinite. A finite sequence is when the domain is the set {1,2,3,...,n} and an infinite sequence is a sequence whose domain is the set of all natural numbers. An arithmetic sequence is a sequence in which each term after the first term is obtained by adding a fixed number, the common difference, to the previous term. A geometric sequence is a sequence in which each term after the first term is obtained by multiplying the preceding term by a constant nonzero real number, called the common ratio.

Some examples of arithmetic sequences

The following is an example of the arithmetic sequence 4n and variations of this sequence.

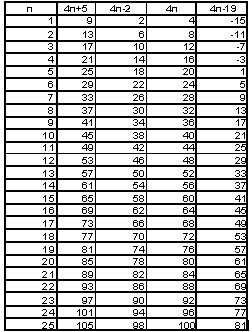
If we look at the graphs of these sequences, we notice that they are all linear. The black line is the graph of 4n+5. The blue line is the graph of 4n. The green line is the graph of 4n-2 and the red line is the graph of 4n-19.

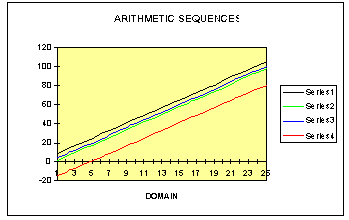
Do all arithmetic sequences have linear graphs? Let's examine another arithmetic sequence to see if its graph is linear. We are going to examine the sequence 1/2n and variations of this sequence. Examine the following spreadsheet.

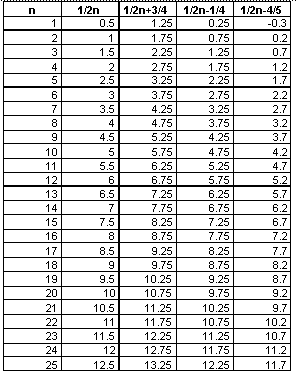
From examining the spreadsheet and from our knowledge of functions and graphs, these sequences appear to have linear graphs also. Let's graph them to find out.

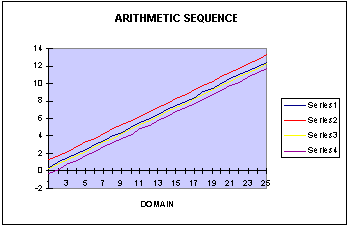
Our hunch was right. These sequences have linear graphs. The red line is the graph of 1/2n+3/4. The blue line is the graph of 1/2n. The yellow line is the graph of 1/2n-1/4. The purple line is the graph of 1/2n-4/5. What can you conclude about arithmetic sequences? Are they all linear? How are these sequences related to other functions?

Examples of Geometric Sequences

The following geometric sequences are 2^n and variations on this sequence.

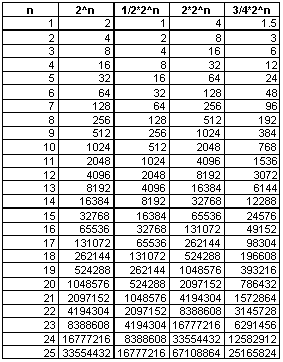
Now, graph these sequences to determine their shape.



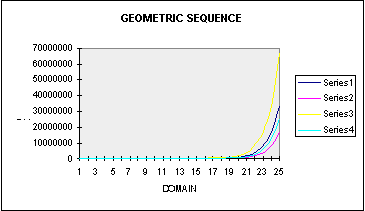
From observing the above graphs, the shape of these geometric sequences are exponential. Let's do another example. In this example, we are investigating the sequence of (1/3)^n and variations on it. Look at the following spreadsheet.

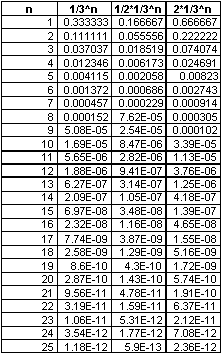
Are the graphs of these geometric sequences similar to the graphs of the above geometric sequences? Let's graph them to see.

The graphs of these sequences have a similar shape to the previous ones. But unlike the previous ones, these graphs are decreasing exponentially; whereas, the previous ones were increasing exponentially. Will all geometric sequences be exponential? How are these sequences related to other functions?

Hopefully, by studying the graphs of different sequences, students will obtain a better understanding of sequences and how they are related to other functions.

Return to HOME PAGE