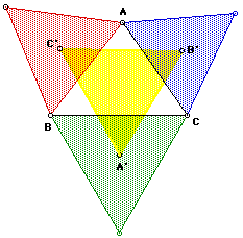

Napoleon's triangle is the yellow triangle. This yellow triangle is equilateral.
Whenever the centers of equilateral triangles are connected, we get an
equilateral triangle.
Investigations of Napoleon's Triangle
Let's see what happens to Napoleon's triangle for various original triangles.
First, let's examine what happens when the original triangle is equilateral.
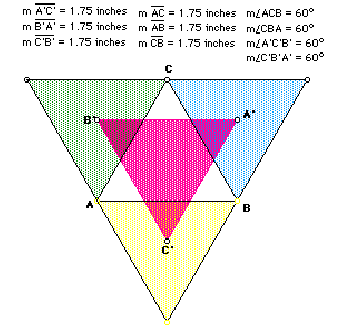
From observing the above diagram, one notices that Napoleon's triangle is
congruent to the original triangle by the AAA postulate. Similarly, Napoleon's
triangle is congruent to the exterior triangles. Now, let's see what happens
when the original triangle is isosceles.
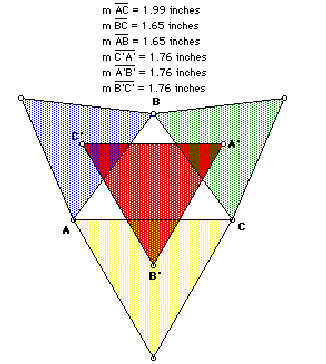
Again, Napoleon's triangle, the red triangle, is equilateral.
What happens when the original triangle is a right triangle?
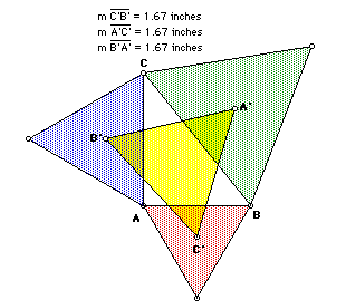
Again, Napoleon's triangle, the yellow triangle, is equilateral.
In all of the cases that I have explored, Napoleon's triangle was always
equilateral.