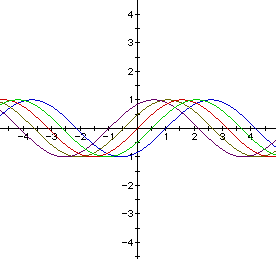
The following graphs show what happens when we change c.
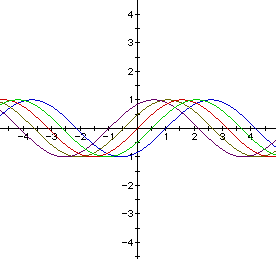
By observing these graphs, one can see that if we keep a=b=1 and change
c the normal sine curve is shifted left or right depending on if c is positive
or negative.
Now lets see what happens when we change a and let b=1 and c=0. Now we are
graphing the equation
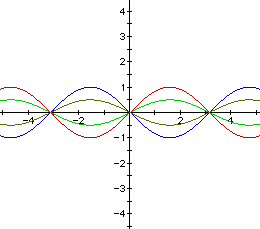
From these graphs, one comes to the conclusion that any change in a will
change the amplitude of the sine curve.
So far we have found out what happens to the graph of y=asin(bx+c) when
we change either a or c and keep the other two constant. Now we need to
see what happens when we change b and let a=1 and c=0. Now we are graphing
the following equation:
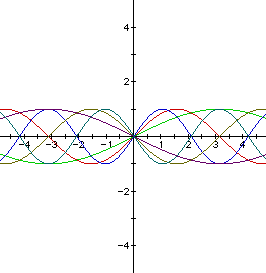
From these graphs, one can see that b stretches or shrinks the period
of the sine curve. If -1<b<1, then the period of the sine curve is
larger. If b>1 or b<-1, then the period is smaller.
What happens to the graph when we change two of the variables and keep the
third one constant? Will let's find out. First, let's examine what happens
when we change a and b and let c=0. The equation that we are using now is
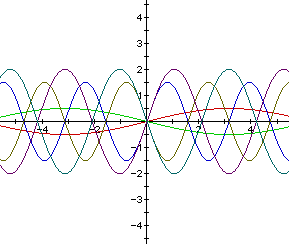
From looking at these graphs, we can see that the graph has been changed
in the same manner as the above graphs. The only difference is that both
the period and the amplitude have changed simultanously.
Now, let b=1 and change a and c. So we are investigating the equation
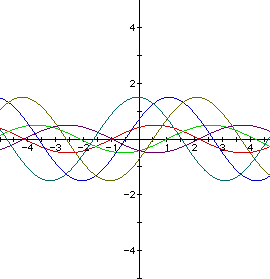
As you can see, when we change a and c the graph shifts and the amplitude
changes.
What changes would you expect if we changed all of the variables? Let's
find out. Now we are experimenting with the equation
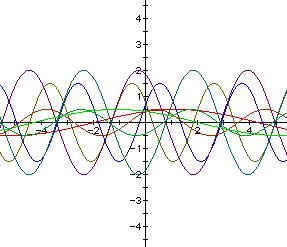
As one can see from the above graph, changing a, b, and c simultanously
changes the graph in three different ways. The graph is shifted left or
right and the amplitude and period changes according to the changes of a
and b.
In the equation y=asin(bx+c), the variables a, b, and c all change the location
and size of the original sin graph. "a" changes the amplitude,"b"
changes the period, and "c" shifts the graph left or right.