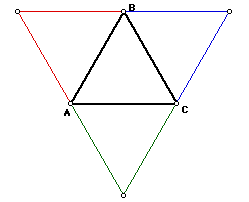

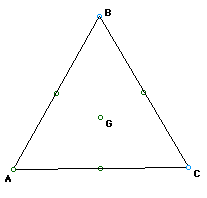
Now, we need to locate the centroid of triangle ABC. From prior constructions,
we know that in order to locate the centroid of a triangle we first need
to find the midpoint of each side of the triangle. Next, we need to join
the midpoints of each side to the opposite vertex. We also know that these
medians are concurrent. Now, we need to find the centroids of the external
triangles, using the same method. We get the following construction.
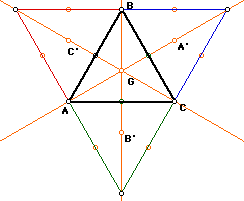
By observing the above construction, one can see the relationship of
the centroids of the external triangles with the centroid of the original
triangle. In this construction, the points A', B', and C' are the centroids
of the external equilateral triangles. Also by observing this, you can see
that the lines AA', BB', and CC' all pass through the centroid of the original
triangle, point G. Since G is the point of intersection of these median
segments, they are concurrent at this point.
Now, let's see if this holds true for any triangle ABC. Let's construct
a scalene triangle and its external equilateral triangles on each side.
Now we need to locate the centroid of each of these triangles. G is the
centroid for triangle ABC and A', B', and C' are the centroids of the external
triangles. If the lines AA', BB', and CC' intersect at G, then G is the
point of concurrency.
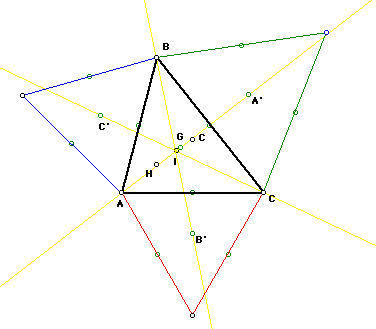
By observing the above construction, one notices that G is not the point
of concurrency in this case. Let's construct the rest of the rest of our
centers (i.e. the incenter (I), the orthocenter (H), and the circumcenter
(C)) to see if one of these points is the point of concurrency for these
lines. It looks like the incenter is the point of currency, but through
further investigation we notice that none of these points are the point
of concurrency. Hence, the point of concurrency does not lie on Euler's
Line.
We can further our investigation of the centers of triangles by constructing
a square externally to each side of the triangle ABC. Next, we need to find
the centers A', B', and C' of each square and construct the lines AA', BB',
and CC'.
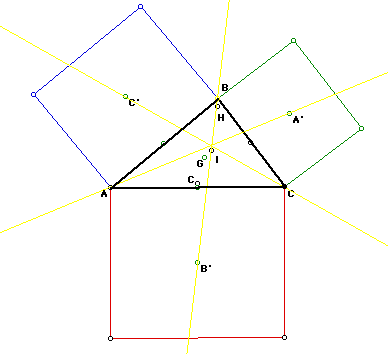
By observation, one notices that these lines do not intersect at the
centroid G of the triangle. Hence G is not the point of concurrency. One
can also observe that the point of concurrency is not any of the points
on Euler's line (i.e. it is not the incenter, the orthocenter, the cicumcenter,
the centroid).
We started our investigation of the centers of triangles by observing equilateral
triangles that were constructed off of each side of the equilateral triangle
ABC, where A', B', and C' were the centroids of the external triangles.
Now, we are going to explore these same triangles but now A', B', and C'
are the external vertices of the external equilateral triangles.
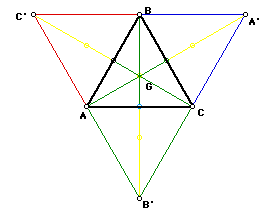
As in the previous investigation, the lines AA', BB', and CC' are concurrent
and the point of concurrency is the centroid G of triangle ABC.
What happens if we begin with a scalene triangle ABC instead of an equilateral
triangle ABC?
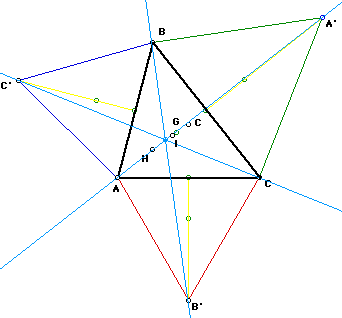
From observing the above construction, you can see that the lines AA',
BB', and CC' are concurrent, but the point of concurrency is not any of
the centers of the triangle ABC.
Now, we are going to see what happens to the point of concurrency when we
construct isosceles triangles having a height equal to the side that it
is constructed on.
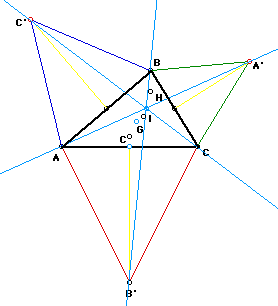
As you can observe, the lines AA', BB', and CC' are concurrent, but their
point of concurrency does not lie on Euler's line.
Now, lets investigate what happens to the point of concurrency when we construct
equilateral triangles toward the center of the original triangle ABC. In
this investigation, A', B', and C' are once again the centroids of the equilateral
triangles.
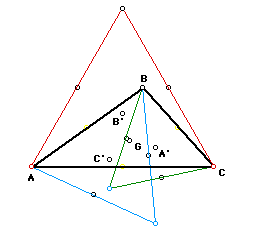
By observation, it is obvious that these triangles are not concurrent
through the centroids of each of these triangles. They are also not concurrent
to any of the other centers of the original triangle. There is one exception
to this. When the original triangle is an equilateral triangle, then they
are all concurrent through the centroids of each of the triangles.
In the above construction, G is the centroid for all of the triangles.
One can continue further investigations of these figures. One can see
if any of the triangles, angles, or sides are similar or congruent. For
example, consider the following construction.
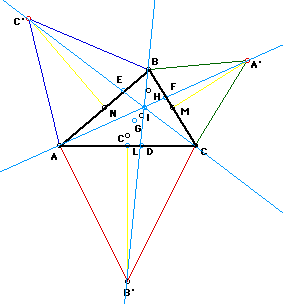
This construction consists of isosceles triangles constructed on each
side of the triangle ABC. Since the external triangles are isosceles, the
triangles AB'L and CB'L are congruent, the triangle AC'N is congruent to
BC'N, and triangle BA'M is congruent to CA'M. These are only a few of the
extensions that one could investigate.
From the above investigations, we saw that the centers of triangles are
related to the centers of other figures that are constructed externally
to the original triangle. Sometimes the centers of the original triangle
are the point of concurrency for the lines that are are constructed from
the center of the external figure to the opposite vertex of the original
triangle and sometimes they are not.