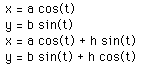
In the above equations, a and b can be any value and h is any real number.
For these equations, we are going to investigate what happens when a=b,
a<b, and a>b. When we use the program X-Functions, we obtain the following
graphs when we change a and b and let t run from 0 to 2*pi.
First, we are going to examine equations x=acos(t) and y=bsin(t).
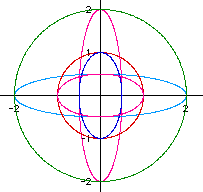
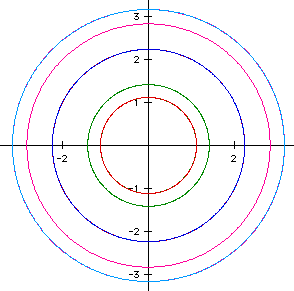
By observing the above figures, you notice that we have circles and ellipses.
Why is this? Let's look at the equations for these figues. The red circle
is the graph of x=cos(t) and y=sin(t). The green circle is the graph of
the equations x=2cos(t) and y=2sin(t). By observing these two graphs and
equations, one notices that if a=b then we get a perfect circle with the
length of the radius being the same as the value for a and b. The longer
fushia ellipse and the dark blue ellipse demonstrate what happens when a<b.
The equation for the fushia ellipse is x=1/2cos(t) and y=2sin(t) and the
equation for the blue ellipse is x=1/2cos(t) and y=sin(t). The light blue
ellipse and the smaller fushia ellipse demonstrate what happens when a>b.
The equations of these ellipses are (x=2cos(t) , y=1/2sin(t)) and (x=cos(t),
y=1/2sin(t)) respectively. Thus, if a>b then the ellipse is elongated
along the x axis and if a<b then the ellipse is elongated along the y
axis. From our observations, one notices that a and b determine the size
of the shape of the figure. It will be either an ellipse or a circle.
Now, lets examine our second two equations.
First, lets examine what happens when we change a and b and fix h.
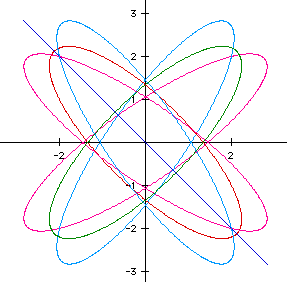
In the above graphs, I let h=-2 and I changed the values for a and b.
I used the following values for a and b {-2,-1,-1/2,1/2,1,2}. We observe
that some of the ellipses are postioned in a positve direction and some
are postioned in a negative direction. The equation for the line is (x=2cos(t)-2sin(t),
y=2sin(t)-2cos(t)). From observing this line, it seems that if a and b are
positive and h is negative, then the figure is going to be postioned in
the second and fourth quadrants. Let's see if this is true. The equations
for the blue ellipses are (x=-1/2cos(t)-2sin(t), y=-2sin(t)-2cos(t)) and
(x=1/2cos(t)-2sin(t), y=2sin(t)-2cos(t)). So which one is negative and which
one is positive? The positive one is the one where a,b, and h are all negative.
The same is true for the other ellipses as well. The fushia ellipses have
the equations (x=-2cos(t)-2sin(t), y=(-1/2sin(t)-2cos(t)) and
(x=2cos(t)-2sin(t), y=(1/2sin(t)-2cos(t)). The equations for the red and
green ellipses are
(x=cos(t)-2sin(t), y=sin(t)-2cos(t)) and (x=-cos(t)-2sin(t), y=-sin(t)-2cos(t)).
In these graphs a and b determine the postion of the ellipse. If a<b,
then they are postioned more toward the
y axis. If a>b, then they are closer to the x axis. If a=b, then the
ellipses are in the center of the first and third quadrant or in the center
of the second and forth quadrant.
Now let's see what happens when a=1/2, b=1, and we change h in the above
equations. We get the following graphs.
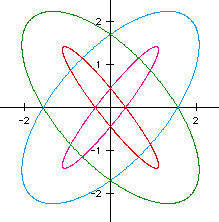
By observing these graphs, it appears that if we keep a and b the same
and change h then the size and postion of the ellipse change when h changes.
The h value for the green ellipse is -2, for the blue ellipse 2, for the
fushia ellipse 1, and for the red ellipse -1. As you can see, when we changed
h from 1 to 2 the ellipse "grew" and when we changed h for 1 to
-1 it rotated 90 degrees.
Now let's see what happens when we let a=1, b=1/2, and h={-3,-2,-1,1,2,3}.
We get the following graphs.
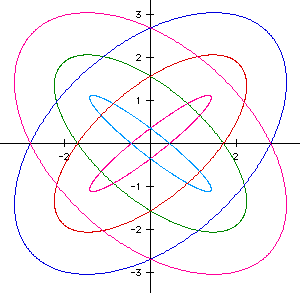
The ellipses have the following h values:
Ellipse Color h Value
smaller fushia 1
red 2
blue 3
light blue -1
green -2
large fushia -3
By comparing these ellipses to the ellipses in the above problem, we notice
that the postioning of the ellipse depends on if a>b or a<b. If a>b
as in the above ellipses, then they are postioned closer to the x axis.
If a<b as in the ellipses prior to these, then they are postioned closer
to the
y axis. We also notice that the ellipses who have the same h value in these
two graphs seem to be the same size. Let's make a chart to show the comparisons.
The ellipses that are side by side are the ones that appear to be the same
size.

In the chart, graph 1 is the graph where a=1/2 and b=1 and graph 2 is the
graph where a=1 and b=1/2. As you notice, the ellipses that are the same
size have the same h value.
Now, lets see what happens when we let a=b=(+ or -)h. In our first set of
ellipses, we noticed that if a=b=-h then we had an equation of a line. Let's
see if this holds true for all instances.
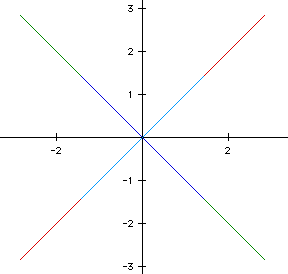
This holds true when a=b and h=(+ or -)a. The above lines have the following
values for a, b, and h.
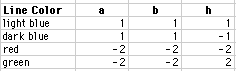
As you notice, if a=b=h then all of the lines lie on the same path. The
path that bisects the first and third quadrant (the path y=x). If a=b=-h,
then all of the lines lie on the path that bisects the second and fourth
quadrant (the path y=-x).
What happens when a=-b and h is changing?
From observing these figures, one notices that they are all circles.
Thus, if a=-b then we will get a circle no matter what h is. We have the
following values for a, b, and h in the above circles.

These are only a few of the investigations that one can perform. There are
many other investigations that one can perform on these equations.