

have 3 real roots? Extend for other values of q (q = 1 in the above equation).
Summarize.
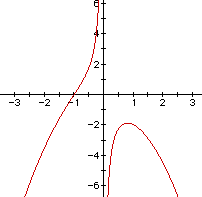
Consider what happens when p = -3.
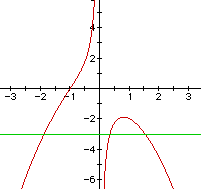
The line crosses the graph in 3 places, each of which is a root. The
first value of p which gives 3 roots is between -1.5 and -2.5 (I'm just
eyeballing the values). When the horizontal line is tangent to the curve
on the right, there will be two roots. When the x value is greater than
that, there will be only one root. Everything less than this value (whatever
it is) will give me 3 roots. Let's see if we can get more exact.
Here are several graphs for different q (still in the xp plane).
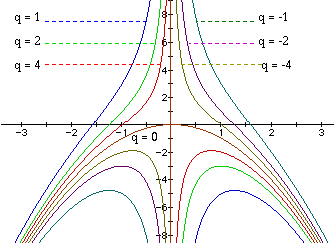
Let's look at the locus of these maximum points, the graph will be a
parabola like this:
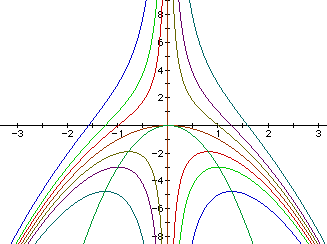
This parabola is the equation
This equation shows us all the p values on one graph, instead of having
to graph each one with different q.