

It has now become a rather standard exercise, with available technology,
to construct graphs to consider the equation
![]()
and to overlay several graphs of
![]()
for different values of a, b, or c as the other two are held constant.
From these graphs, students will be able to make many conjectures about
the characteristics of a, b, and c.
A discussion of the patterns of the roots can be very useful. For example,
if we set
![]()
for b = -3, -2, -1, 0, 1, 2, 3, and (after viewing each graph separately)
overlay the graphs, we obtain the following picture.
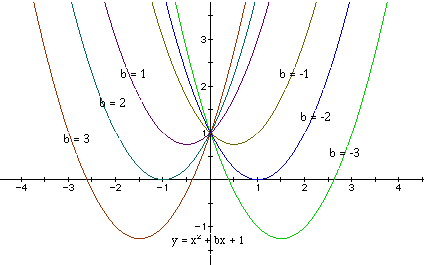
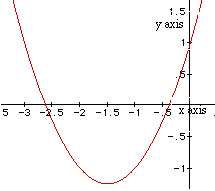
Students should be able to discuss the "movement" of the parabola
as b is changed. A meaningful discussion of this family of graphs will be
the bridge to all similar families. Can students determine what points on
the graph are important? One point on the graph is common to all the parabolas,
the point (0, 1) . This is completely as we would expect when we examine
the equations used.
The roots of the equations can be seen along the x-axis. Can the students
make general comments about what sorts of roots the equations have either
by looking at the equation or (of particular interest) by looking at the
picture? And can they understand what it means on the graph when
they find roots of the equation ?
For b < -2, the parabola will intersect the x-axis in two points with
positive x values (i.e. the original equation will have positive real roots).
For b = -2 and b = 2, the parabola is tangent to the x-axis and so the original
equation has one real and positive root at the point of tangency. For -1
< b < 2, the parabola does not intersect the x-axis -- the original
equation has no real roots. And for b > 2, the parabola intersects the
x-axis twice to show two negative real roots for each b. This all begs the
question "What is a root?" Can students answer this question?
And once they know this with great certainty, do they know why a quadratic
may have one or no real roots? These are items which I have found painfully
lacking in students' repertoires.
Having successfully mastered all this , consider the locus of the vertices
of the set of parabolas graphed from
![]()
The locus is, in fact, a parabola with the equation
![]()
The general form for this equation is
![]()
for any family of graphs.
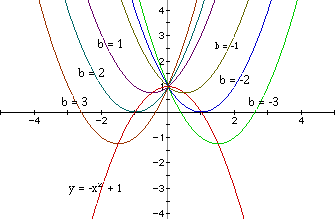
Now we can see even better the next location of the parabola in the family
(b = 4 or b = -4).
Consider again the equation
![]()
Graph this relation in the xb plane.
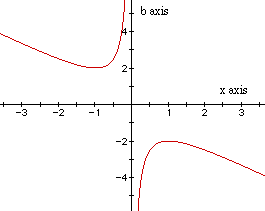
Naturally, the graph is a hyperbola (the two variables are x and b).
If we take any particular value of b, say b = 3 and overlay this equation
on the graph, we add a line parallel to the x-axis. The points of intersection
of the curve and the line (in the xb plane) give the roots of the original
equation.
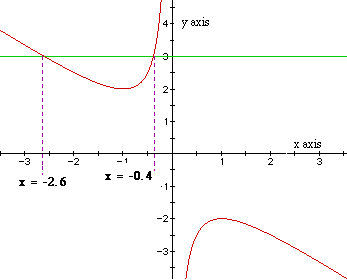
The approximate roots of the equation then when b = 3 are -2.6 and -0.4,
which can be seen back in the xy plane.
Looking back at the equation in the xb plane
![]()
we can make hypotheses about the roots without necessarily graphing so
many members of the family.
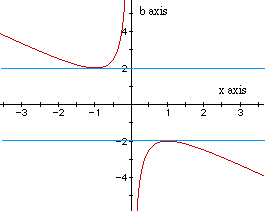
The top blue line is where b = 2. If b > 2, x is negative and has
two intersection points with the line. This means in the xy plane the parabola
has two negative real roots. If b < -2, x is positive and has two intersection
points with the line. Then in the xy plane the parabola has two positive
real roots. If b = 2 , then x = -1. If b = -2, then x = 1. Therefore, at
these two values of b, x has one real root (one negative and one positive,
respectively). If -2 < b < 2, there are no intersection points, so
there are no real roots between these values of b. The line x = 0 is asymptotic
to the hyperbola because if x = 0 in the equation
![]()
then it reduces to 1 = 0. This means there are no roots at x = 1. This
is as we would expect since in the above graph in the xy plane where b ranges
from -3 to 3, all the parabolas go through x = 1. There exists roots at
every number on the x axis on either side of 1, but not including 1.
![]()
Similar to above, if the equation is graphed in the xc plane, certainly
the graph will be a parabola. Overlaying any value of c, will give a line
crossing this parabola in 0, 1, or 2 points. The intersection points are
the roots of the original equation at that value of c. Observe the graph
when c = 1, then
![]()
will have two negative roots -- approximately -0.2 and -4.8.
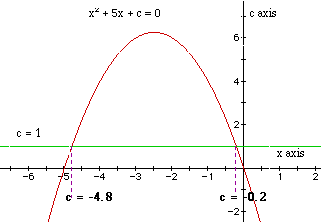
Consider the parabola above while sliding the green line up and down
the graph. There is one value of c where the equation will have only 1 real
root -- at c = 6.25, the green line will intersect the parabola in one point.
For c > 6.25, the green line will not intersect the parabola, the equation
will have no real roots. For c < 6.25, the green line will intersect
the parabola in two points. Both these x values will be positive for 0 <
c < 6.25. When c = 0, x (or the roots of the original equation) will
be -5 and 0. When c < 0, there will be one positive root and one negative
root.
![]()
if you hold c constant (for example, c = 1) then the graph in the xb
plane will show the roots of the original equation for different values
of b. Likewise, holding b constant (for example, b = 5) then the graph in
the xc plane also shows the roots of the original equation for different
values of c. In examining the original problem in different ways, students
will gain great insight into the mathematics.