Write up #3

Take any triangle ABC. Construct equilateral triangles externally on each side and loce the centroid of each equilateral triangle (label A' for the centroid opposite vertex A, etc.). Construct lines AA', BB', CC'.

These three lines are concurrent.

Conjectures:

Construct the triangle through the outer vertex of each of the three equilateral triangles, call this triangle XYZ. Draw Euler's line for triangle XYZ. (This line goes through the circumcenter and the orthocenter and the centroid).

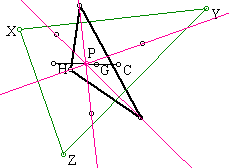
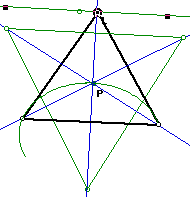
As you see the point of concurrency in question, P, is on the Euler Line for the triangle XYZ. There exist many interesting ratios on this line.

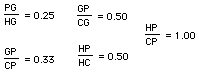
This point of concurrency, P, is the midpoint of Euler's line in triangle XYZ. This means that the center of the nine point circle which circumscribes triangle XYZ is the point P.

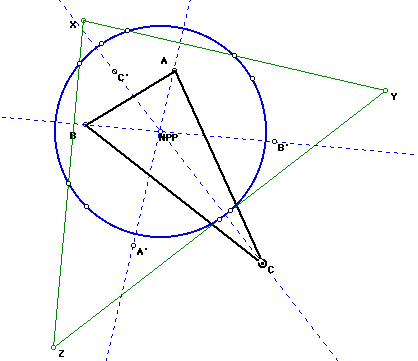
The point labeled NP is the center of the nine point circle. The other P is the label (for the same point) which is the point of concurrency in question.

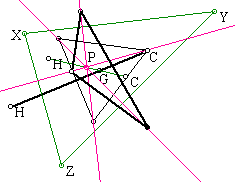
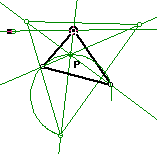
The Euler line of the triangle A'B'C' is more specifically named the Euler "point" because this triangle is equilateral, and all centers are the same for equilateral triangles. The Euler line for triangle ABC intersects the Euler line of XYZ at the Euler "point" of triangle A'B'C'.

When we construct a line through one of the vertices, say A, and find the locus of point P, we see that it seems to be an ellipse but it never actually closes. If you could finish drawing the ellipse, it would pass through two vertices (in this case, A and B) of the original triangle and the centroid (in this case, C') of the equilateral triangle made of the side containing those two vertices. Sometimes the "ellipse" will go through the third vertex of the original triangle also (C), that is, when angle ACB is big enough.

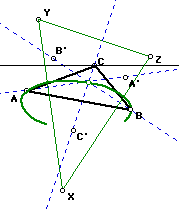
At a certain point where an angle is around 120 degrees, the ellipse changes to a hyperbola, which seems to always pass through two vertices.

Repeat the investigation using a square constructed externally on each side of triangle ABC and with A', B', C' being the centers of the squares.

Construct triangle A'B'C'. The point of concurrency, P, is also the orthocenter of that triangle. The centroid of triangle ABC is the same as the centroid of triangle A'B'C'. Then the Euler lines for these two triangles intersect at these common centroids (G).

The interesting ratios are still there just by nature of the Euler line itself.

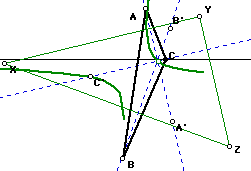
Looking at a trace of P in this situation, we see what appears to be another open ellipse, going through at least two vertices. (Triangle A'B'C' is still green, the squares on each side are hidden in the interest of space.)

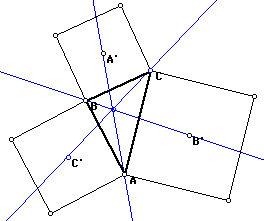
Repeat the investigation but let A', B', and C' be the external vertices of the externally constructed equilateral triangles.

Again, looking at the trace, we see that when a vertex traces a line, the point P will trace almost a circle.

In fact, to look at ANY case, make a construction so that you can vary the angle ABC'.

If you construct an equilateral triangle on each side of ABC, then the angle BAC' will be 30 degrees. And likewise for each side.

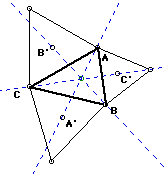
If you construct a square on each side of ABC, then the angle BAC' will be 45 degrees. If C' is the external vertex of an equilateral triangle, angle BAC' will be 60 degrees.

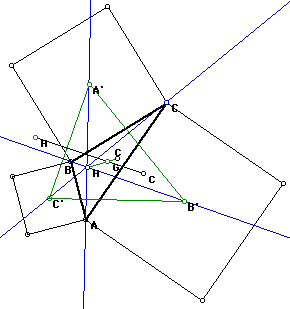
That center point (not P but the A', B', or C') is just located at different points along the perpendicular bisector. Rotate a side from 0 degrees to 90 degrees around a fixed vertex and the intersection of that side and the perpendicular bisector will be A', B', or C'.

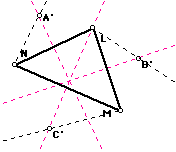
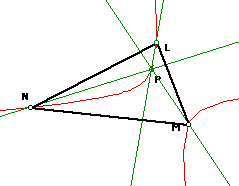
The angles L, M, and N are the ones formed when the sides are rotated. The pink dotted lines are the perpendicular bisectors, so the point of intersection shown here is the circumcenter.

Click here to explore the construction.

Now to explore this a moment, we can trace the locus of P as we vary the "MARKED angle".

For this specific triangle ABC, the locus of P as the angle varies (i.e., the points A', B', and C' move up the perpendicular bisector), is a hyperbola.

Click here to see the locus traces. Drag any vertex of the original triangle.

Isn't that cool?

Return to Sherry's class page