

NOTE: Enlarge your screen to the largest, please. The pictures will fit two per line!
![]()
How would you change the equations to explore other graphs?
![]() .
.
If we can look at the cosine and sine curves graphed on the same set of axes, we can easily find the ordered pairs we want for this new parametric curve. (Click here if you want to see this GSP sketch.)
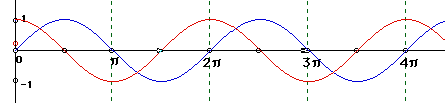
The red curve corresponds to cosine, and the blue is sine. The horizontal axis is the value of t for the parametric curve, while the vertical axis will give the cosine and sine value as needed. For example, look at t = pi. The cosine value at pi is on the red curve (in fact, for this particular point, it is where the dotted green line intersects the red curve) at -1 on the vertical axis. The sine value at pi is on the blue curve (where the dotted green line intersects the blue curve) at 0 on the vertical axis. Then the ordered pair for the parametric curve is
![]()
and to find several ordered pairs for the new graph:
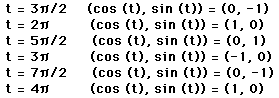
This graph will be a unit circle.
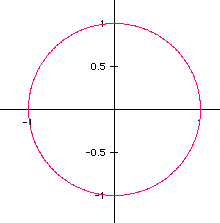
This will always be the graph for the given x and y. Changing t will only cause the trace of the same curve.
Now if we change the graph to be
![]()
take the ordered pairs above and multiply by a and b respectively.
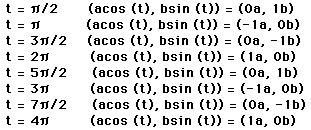
Take a look at what happens when a = 2 and b = 5.
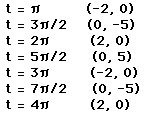
So the corresponding graph --
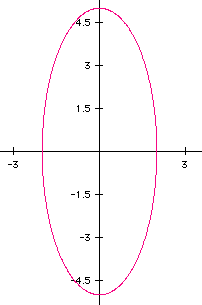
This ellipse has y as the major axis with length 2 * 5 and x is the minor axis with length 2 * 2.
Here are other graphs with different a and b.
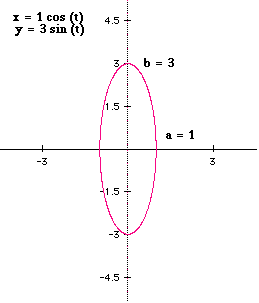
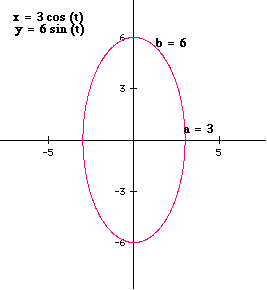
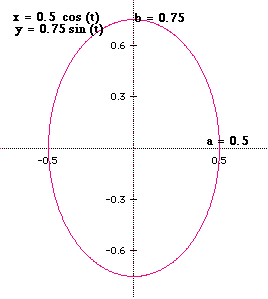
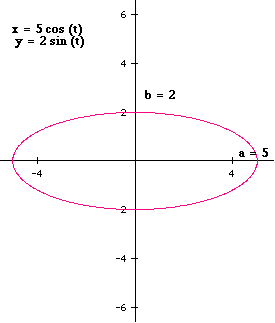
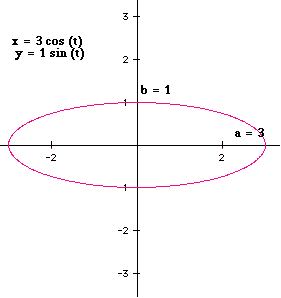
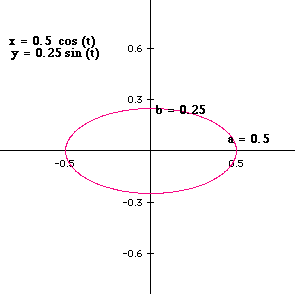
At this point we may conclude |a| (any a, positive or negative) gives the "endpoints" on the x axis and b (any b, positive or negative) gives the "endpoints" on the y axis.
When |a| < |b|, the graph will be an ellipse and the major axis will be the y axis.
When |a| > |b|, the graph will be an ellipse and the major axis will be the x axis.
When |a| = |b|, the graph will be a circle.
Cos (t) ranges from -1 to 1, so a cos (t) ranges from -a to a; similarly, b sin(t) ranges from -b to b. This gives the x and y axis ranges. The value of t will still be from 0 to 2pi.