(equation 1)
where we varied a, b, or c and held the other two constant. We chose
to use Algebra Xpresser for this investigation.
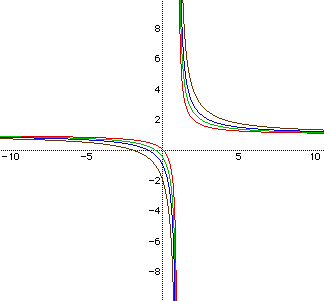
As c increases, the hyperbolas move away from the origin, and they become
more narrow.
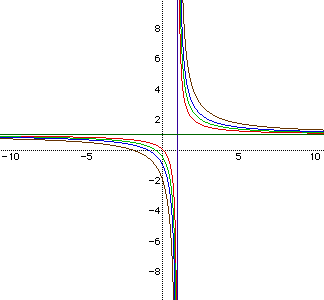
These two lines (purple and green) look like the asymptotes. We investigated
further by solving the initial equation for y and then x and graphing the
resulting equations. Solving for y, we obtain the equation,
Again, we allowed a=b=1 and c=0, 0.5, 1, and 2. See graphs below.
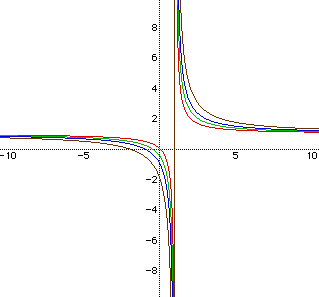
The tan vertical line is x-1=0 and acts like one of the asymptotes of
the family of hyperbolas. If we look at equation 2, we see that it is not
defined when x-1=0, since we cannot have a zero in the denominator. So the
hyperbolas get closer and closer to the line x-1=0, but never reach it (i.e.,
the definition of an asymptote).
Again, we allowed a=b=1 and c=0, 0.5, 1, and 2. See graphs below.
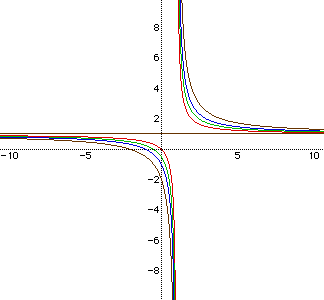
The tan horizontal line is y-1=0 and acts like the other asymptote of
the family of hyperbolas. If we look at equation 3, we see that it is not
defined when y-1=0, since we cannot have a zero in the denominator. So the
hyperbolas get closer and closer to the line y-1=0, but never reach it (i.e.,
the definition of an asymptote). (Further investigations will be done only
with equation 1.)
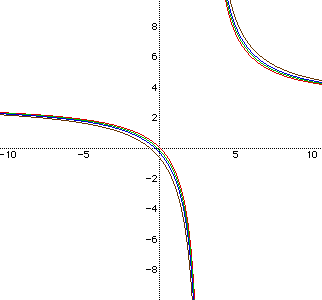
From the discussion above, we assume that x - b = 0 and y - a = 0 are
the asymptotes (where a = b = 3 in this case). The graph below verifies
this.

Below we examine graphs for a = b = 1, a = b = 3 , a = b = 4 ,and c =
0.
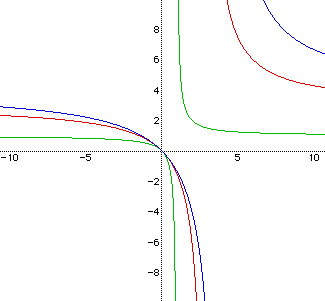
As a and b increase, the upper hyperbolas move away from the origin,
but the lower halves still go through the origin. Also, the hyperbolas widen
as a and b increase.
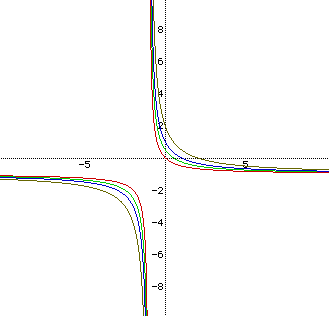
For thoroughness, we then looked at a = b = -3 and c = 0, 0.5, 1, and
2.
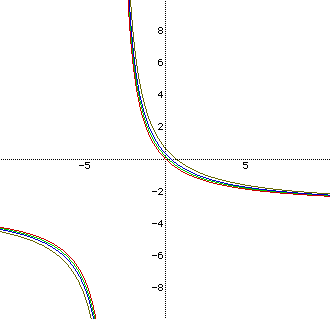
It appears that negative values of a and b shift the hyperbolas down
and to the left, while smaller values widen the hyperbolas. Thus when a
and b are positive, larger values widen the hyperbolas, and when a and b
are negative, smaller values widen the hyperbolas. In general, if the absolute
value of a and b increases, the hyperbolas will widen. Also as the absolute
value of a and b increase, the lower halves of the hyperbolas move away
from the origin.
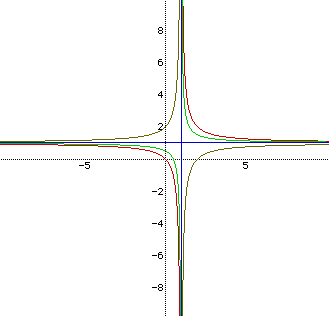
The blue lines (where c = -1) look like asymptotes to these hyperbolas.
However upon closer inspection of this equation we saw that,
which is defined everywhere. Since the asymptotes of these hyperbolas
are x-1=0 and 1-y=0 (see reasoning above), we see that the blue lines lie
on top of the asymptotes.
We also noticed that when c=-2 (the tan lines, above) the hyperbola moves
into the second and fourth quadrants (using the blue lines as our axes).
At first we suspected that the hyperbolas were just reflections of each
other (about x-1=0 or y-1=0) when |c| equaled the same number. We tested
out conjecture by graphing the hyperbolas where c = -2 (red) and c = 2 (green)
and (x-1)(y-1)=0 (blue).
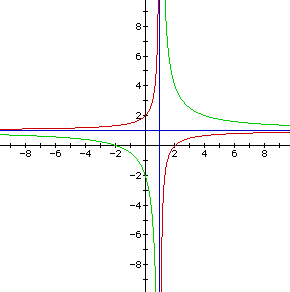
Obviously they are not reflections of each other since the red hyperbola
(c=-2) is narrower than the green hyperbola (c=2). Also the red hyperbola
approaches the lines x-1=0 and y-1=0 faster than the green hyperbola. However,
they do share the same asymptotes.
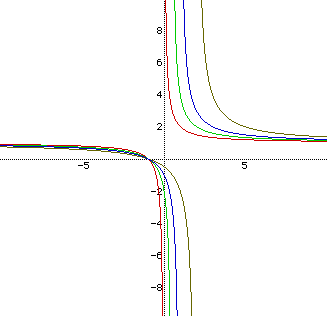
The hyperbolas move to the right, as b increases.
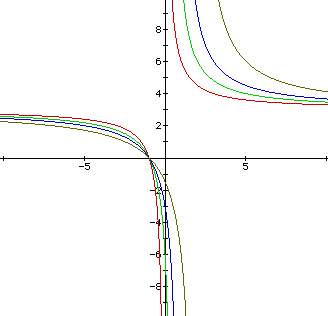
As a and c increase, the hyperbolas widen as they move away from the
origin.
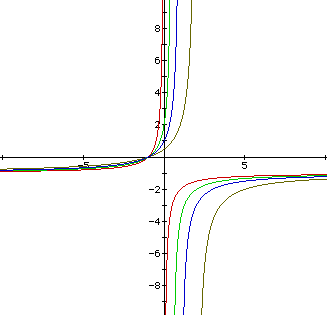
Before we comment on how negative values of a and c affect the hyperbolas,
look at a = c = -3 and b = 0, 0.5, 1, and 2.
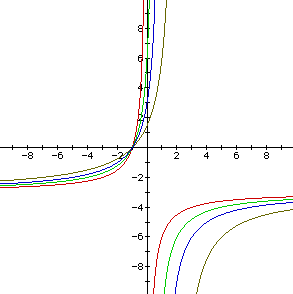
It appears that negative values of a and c flip the hyperbolas about
the origin, and smaller values widen the hyperbolas. Thus when a and c are
positive, larger values widen the hyperbolas, and when a and c are negative,
smaller values widen the hyperbolas as well. In general, as the absolute
value of a and c increases, the hyperbolas widen. Also as the absolute value
of a and c increase, the lower halves of the hyperbolas move away from the
origin.
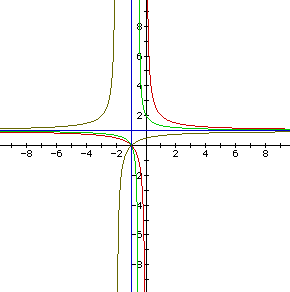
Here only one of the blue lines (where b = -1) looks like an asymptote
to these hyperbolas, namely the horizontal line y-1=0. Since we varied the
coefficient of the y-term, the hyperbolas shift to the left and thus cannot
have the same vertical asymptote. See the following graph to verify.
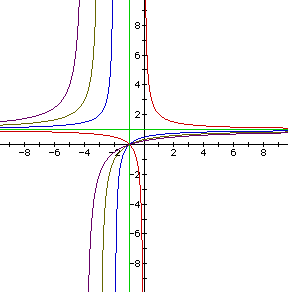
Next we let b = c = 1 and a = 0, 0.5, 1, and 2.
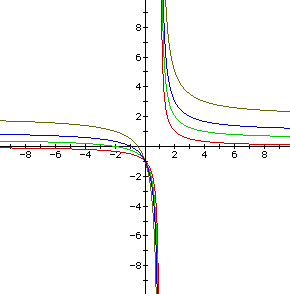
As a increases the lower hyperbolas move upward and slightly to the left,
while the upper hyperbolas move away from the orgin.
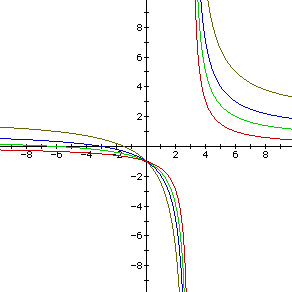
As b and c increase, the upper hyperbolas widen as they move away from
the origin, whereas the lower hyperbolas move upward and slightly to the
left.
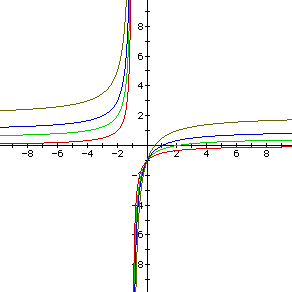
Before we comment on how negative values of b and c affect the hyperbolas,
look at b = c = -3 and a = 0, 0.5, 1, and 2.
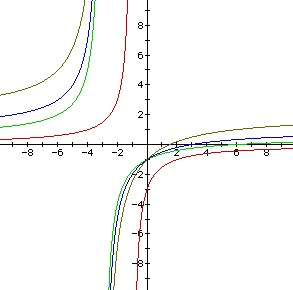
It appears that negative values of b and c flip the hyperbolas about
the origin and smaller values widen the hyperbolas. So when b and c are
positive, larger values widen the hyperbolas, and when b and c are negative,
smaller values also widen the hyperbolas. In general, if the absolute value
of b and c increases, the hyperbolas widen. Also as the absolute value of
b and c increase the lower halves of the hyperbolas move away from the origin.
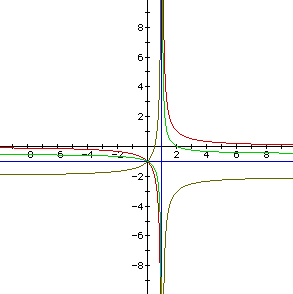
Here only one of the blue lines (where a = -1) looks like an asymptote
to these hyperbolas, namely the horizontal line x-1=0. Since we varied the
coefficient of an x-term, the hyperbolas shift down and thus cannot have
the same horizontal asymptote. See the following graph to verify.
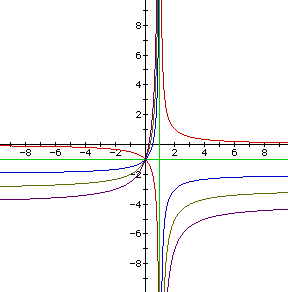
Solving for xy, we obtain our original equation
To investigate we let k = 0, 1, 2, 3 and a = b = 1.
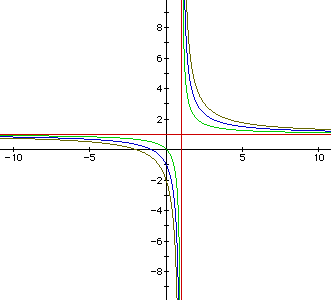
Again we graph, letting k = 0 , -1, -2, -3 and a = b = 1.
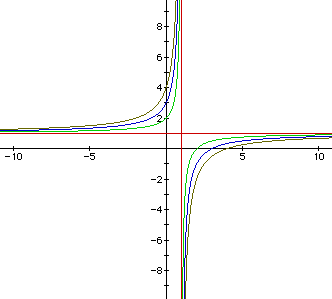
From these two pictures, it appears that if k=0 we get perpendicular
lines. If we look closely at the general equation xy = ax + by + k - ab,
when k = 0, c = -ab. So for our specific equation where
a = b = 1, we have
which factors into
When we graph this equation, we get the perpendicular lines x-1=0 and
y-1=0.
If k![]() 0, then c = k - ab and we get another set of hyperbolas. For our specific
equation where
0, then c = k - ab and we get another set of hyperbolas. For our specific
equation where
a = b = 1, we have
Thus c = k - 1, and for the various values of k![]() 0, we get sets
of hyperbolas.
0, we get sets
of hyperbolas.
So we see that as we vary a, b, or c and hold the other two constant, we
generate a family of hyperbolas that change position and orientation as
well as width. Thus, using technology such as Algebra Xpresser enables students
to more easily investigate families of curves in depth.