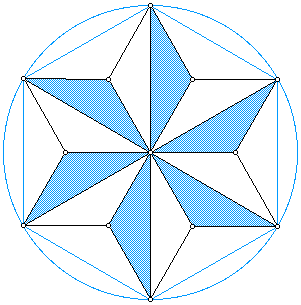
The introduction of such geometric terms as line, line segment, point, angle, and circle terms such as arc, radius, and concentric circle, is enhanced when presented through designs. The simple circle design illustrated here is a circle divided into six arcs using the radius to mark off the circumference. The students then make a regular hexagon, draw diameters and diagonals, and remove construction marks. The second construction is similar but includes a concentric circle with half of the radius of the first.


The creation of tesselations is an activity that reinforces many geometric concepts. Investigating regular tesselations requires angle measures, divisibility of 360, the vocabulary of regular and congruent. If given polygons of congruent shapes students can explore to determine that only those shapes with interior angles that are factors of 360 will form regular tesselations.
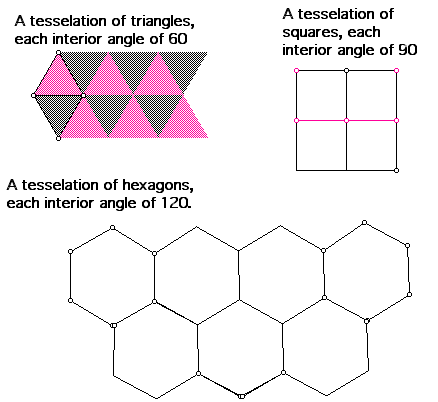
It is often helpful to give examples that will not work. While making very interesting designs, regular pentagons will not tesselate unless combined with other polygons. No matter how they are placed, regular pentagons will always leave gaps of overlap.

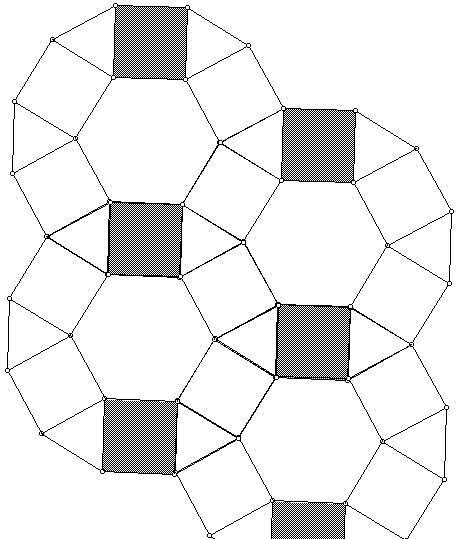
The exploration can be expanded to semi-regular tesselations where the students detemine when a combination of regular polygons will tile a plane.
With the use of dynamic geometry software, repeating a sketch
can give very interesting results. The following was constructed
with repeated use of a script that formed a new triangle by connecting
the midpoints of the previous one.
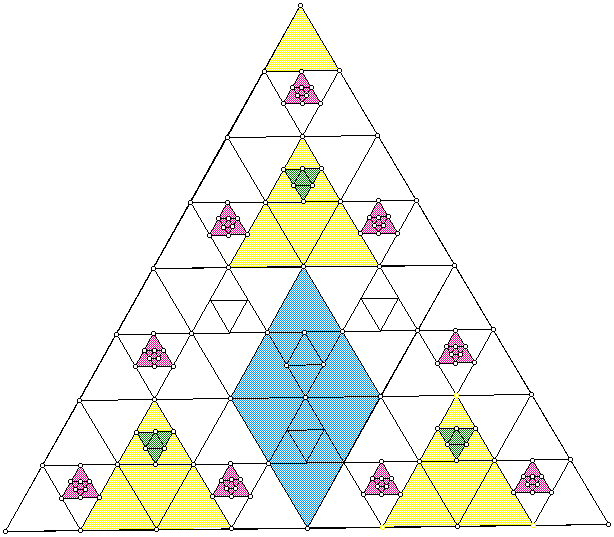
From regular polygons, students can explore rectangles, rhombuses, and other non-regular polygons to make conjectures about what will tesselate. Throughout all of these explorations, the emphasis on mathematical concepts of symmetry, translations, reflections, rotations reinforces these concepts.
A natural progression to Escher-like tesselations can be explored on Geometer's Sketchpad or with a rectangle of paper which is cut from one side and taped to the opposite side. With the GSP construction, students can watch translations from the vectors that they had determined.

More circle designs with inscribed regular polygons made with
either compass and straight edge or with geometry software are
valuable exercises to reinforce the understanding of the properties
of regular polygons, and the properties of a circle.
(Click Here to see a GSP Script
that demonstrates the area and perimeter of these regular polygons.)
With the use of central angles, the students can partition the
circle into sections of equal size, then with joining the endpoints
of selected diameters or radii they can create regular polygons.
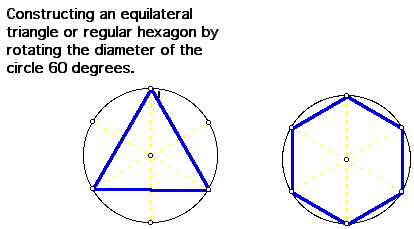
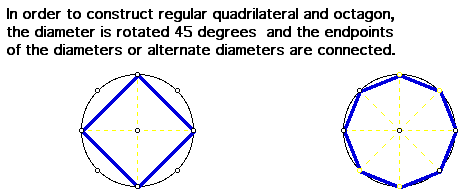
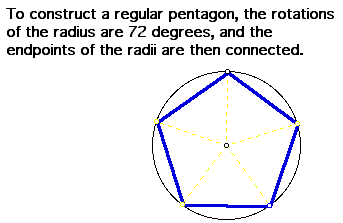
The discussions during all of these constructions can be as involved
as the students in the class are capable of understanding. Using
circles to construct regular polgons offers a variety of mathematical
concepts from dividing into 360 degrees, to the use of radii and
diameters to subtend equal parts of the circle, to approaching
the area of the circle as a limit to the area of the polygon as
the number of sides is increased.
The fun and hands-on approach desguises the learning for many seventh graders. Geometry can be as mathematically intense without the common problems of motivation or student involvement when taught with constructions.