
An exploration with the Golden Ratio offers opportunities to connect an understanding of ratio and proportion to geometry as well as to introduce historic and aesthetic elements to a mathematical concept. The explorations with a spreadsheet demonstrate Fibonacci numbers and the ratio between each pair. The GSP exploration demonstrates how to construct the ratio geometrically. The use of calculators to prove the definition and properties of this ratio are also appropriate.

from Web Page by Ned May(nedmay@Moonstar.com)
History
The name Golden Ratio or Golden Number , named "phi" by the Greeks for the Greek scultor Phidias. However, this ratio can be found in art and architecture long before the Greeks. The Great Pyramid of Giza built around 2560 BC is one of the earliest examples of the use of this ratio. The length of each side of the base is 756 feet, and the height when built was 481 feet. 756/481=1.571725572.

from http://ce.eng.usf.edu/pharos/wonders/Gallery/pyrami.jpg
The Parthenon in Athens Greece, built in 440BC, examplifies the use of the golden rectangle in many of the dimensions. The spaces between the columns, height to width, are in proportion to the golden ratio as are most of the exterior dimensions.

from Encyclopedia Encarta
Geometry
It is easy to find the golden ratio in common shapes today. Some interesting geometric examples can be found in a regular pentagon, "Sublime" triangle and graveyard crosses as illustrated in the following Geometer's Sketchpad constructions.
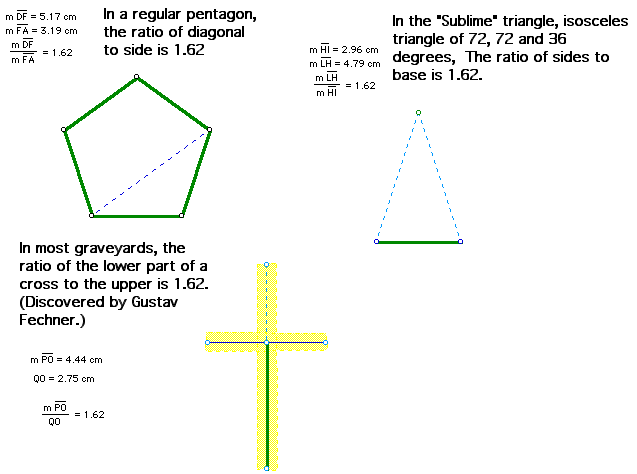
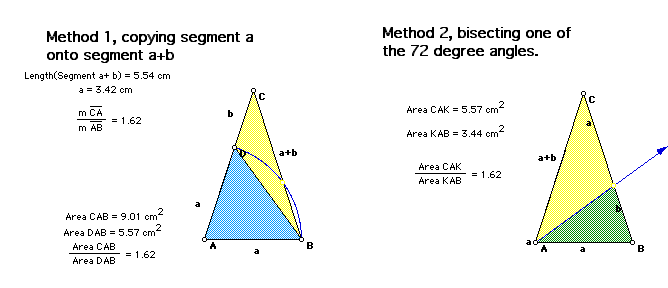
More construction can be done with the "Sublime" triangle to illustrate other properties of the golden ratio. When copying the segment a on to the segment a+b we can see the golden ratio when comparing a+b to a. The areas of the two triangles give the same ratio. Area of the original triangle is to the new one as a+b is to a, both of which are equal to the golden ratio..
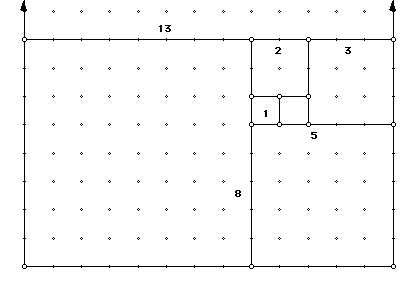
Fibonacci Rectangles and Fibonacci Spiral
Constructing Fibonnaci rectangles by use of Geometer's Sketchpad is relatively easy. Start with a unit square, place another unit square next to it, use this length of 2 as a side for the next square. Where the side of 2 units is adjacent to the 1 unit, construct another square with side of 3 units. Continuing to add squares to the new side, so as each new square has a side the sum of the previous two sides, we can see the Fibonnaci sequence in the lengths of the successive sides.
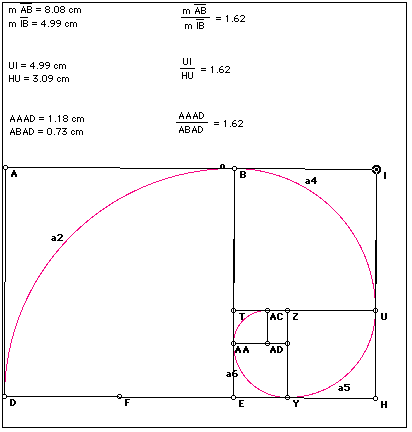
Using Geometer's Sketchpad and starting from the largest square, which is made into a golden rectangle by making its width equal to the diagonal of the square, we can construct another set of Fibonnaci rectangles. This set demonstrates the use of a script. Each rectangle formed by partioning off a square, the rectangle left is then also partitioned into another square and smaller rectangle. Using the measurement tool of GSP, we are able to watch the constant ratio as the rectangles become smaller and smaller. The construction tool also allows us to construct the Fibonacci sequence. The similarity of this shape to some found in nature, such as the cross-section of a Nautilus shell , is a connection to math in science. There are available many web sites that offer activities and illustrations of Fibonacci numbers and nature. They connect Fibonacci numbers and plants, petals on flowers, leaf arrangements, seed heads, and pine cones. (Click here for The Fibonacci Numbers and Nature.)
The Golden Ratio on a Spreadsheet
Using a spreadsheet where the Fibonacci numbers are generated and then put into a ratio of A(n)/A(n-1) demonstrates convergence to a limit, Phi. Column 3 and 4 illustrate other interesting properties of the Fibonnaci Sequence and subsequent ratios. Column 3 compares every third number in the sequence which converges to Phi + 1, and column 4 shows that the ratio of the third term converge to Phi +3.

| FibonacciSequence | Ratio A2/A1 | Ratio A3/A1 | Ratio A4/A1 |
| 1 | |||
| 1 | 1 | ||
| 2 | 2 | 2 | |
| 3 | 1.5 | 3 | 3 |
| 5 | 1.66666666666667 | 2.5 | 5 |
| 8 | 1.6 | 2.66666666666667 | 4 |
| 13 | 1.625 | 2.6 | 4.33333333333333 |
| 21 | 1.61538461538462 | 2.625 | 4.2 |
| 34 | 1.61904761904762 | 2.61538461538462 | 4.25 |
| 55 | 1.61764705882353 | 2.61904761904762 | 4.23076923076923 |
| 89 | 1.61818181818182 | 2.61764705882353 | 4.23809523809524 |
| 144 | 1.61797752808989 | 2.61818181818182 | 4.23529411764706 |
| 233 | 1.61805555555556 | 2.61797752808989 | 4.23636363636364 |
| 377 | 1.61802575107296 | 2.61805555555556 | 4.23595505617978 |
| 610 | 1.61803713527851 | 2.61802575107296 | 4.23611111111111 |
| 987 | 1.61803278688525 | 2.61803713527851 | 4.23605150214592 |
| 1597 | 1.61803444782168 | 2.61803278688525 | 4.23607427055703 |
| 2584 | 1.61803381340013 | 2.61803444782168 | 4.23606557377049 |
| 4181 | 1.61803405572755 | 2.61803381340013 | 4.23606889564336 |
| 6765 | 1.61803396316671 | 2.61803405572755 | 4.23606762680025 |
| 10946 | 1.6180339985218 | 2.61803396316671 | 4.23606811145511 |
| 17711 | 1.61803398501736 | 2.6180339985218 | 4.23606792633341 |
| 28657 | 1.6180339901756 | 2.61803398501736 | 4.23606799704361 |
| 46368 | 1.61803398820532 | 2.6180339901756 | 4.23606797003472 |
| 75025 | 1.6180339889579 | 2.61803398820533 | 4.23606798035119 |
| 121393 | 1.61803398867044 | 2.6180339889579 | 4.23606797641065 |
| 196418 | 1.61803398878024 | 2.61803398867044 | 4.2360679779158 |
| 317811 | 1.6180339887383 | 2.61803398878024 | 4.23606797734089 |
| 514229 | 1.61803398875432 | 2.6180339887383 | 4.23606797756049 |
| 832040 | 1.6180339887482 | 2.61803398875432 | 4.23606797747661 |
Another interesting feature of Phi is that the Lucas numbers, with seed values of 2 and 1, and any other series formed by adding the two latest numbers will converge to Phi when put into a ratio of successive terms.
Finding Phi on a calculator

Summary
There is a world of connections to Phi. There are the obvious connections to the other content areas of nature, history, art and architecture. The mathematical connections between geometry and algebra can be stressed by connecting Phi to the Fibonacci numbers and spiral. There are also connections within the technology with the use of spreadsheets, geometry software, calculators, and the internet.
References:
Ashmawy, A.K., "The great pyramid of Giza", Retrieved 6/27/00 from the World Wide Web, http://ce.eng.usf.edu/pharos/wonders/pyramid.html
Penny Tweedle/Tony Stone Images, (2000), Encyclopedia Encarta
Knott, R., "The Golden section ratio: Phi", Retrieved 6/21/00 from the World Wide Web, http://www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/phi/html#calc
May, N. "Fibonacci", Retrieved 6/20/00 from the World Wide Web, http://www.moonstar.com/-nedmay/chromat/fibonaci.htm
"The Golden Ratio", Retrieved 6/21/00 from the World Wide Web, http://www.geom.umn.edu/~demo5337/s97b/art.htm