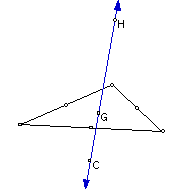

Using the midpoints of the sides of this triangle and rerunning the script
will give the Medial triangle and find the centers for this triangle. Through
the construction, it is obvious that the Medial triangle is similar to the
original, only reflected, so that the H of the Medial triangle coincides
with the C of the original, while Euler's line remains. One could use this
to prove that the 4 triangles formed are congruent so that the ratio of
4:1 exists between the original triangle and the Medial triangle.
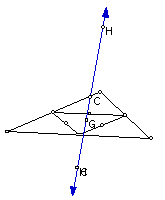
This can be repeated again and again.
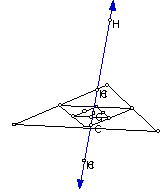
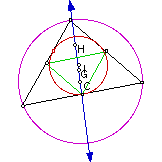
Taking this script and adding steps to construct the circumcircle, incenter
and incircle to the previous constructions shows more properties of a triangle.
The Medial triangle and circumcircle were also added to the script.
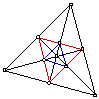
Because this script produces a very busy triangle, it seems logical to
start a new script for the orthocenter, mid-segment triangle and orthic
triangle. In the following sketch, the orthotriangle is constructed in red,
and the mid-segment triangle is in blue.
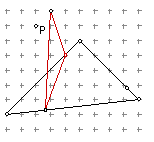
The script for the Pedal triangle gives the opportunity to investigate
Simpson's line. The Pedal triangle is formed by connecting the points at
the feet of the altitudes from P to the respective sides. The script will
give the Pedal triangle, then one can add the circumscircle and animation
to find the deltoid.
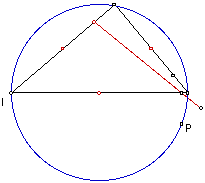
When P is on the circumcircle, the sides of the Pedal triangle coincide,
forming Simpson's line.
When P is on the orthocenter, the Pedal triangle becomes the Medial triangle.
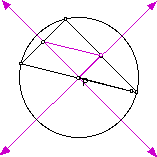
The ninepoint circle is another script that reproduces a rather tedious
construction with ease, that can then be manipulated to watch interesting
changes.

Other Scripts:
Trisecting a line segment with parallel lines.
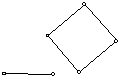
Constructing a square, given a line segment and location.
Constructing an equilateral triangle given a line segment and location.