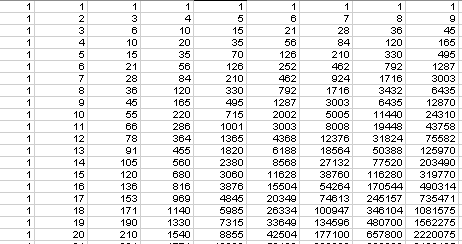
The patterns presented in Pascal's triangle can be used to review multiples, factors, and other concepts presented in a unit on number theory for a seventh grade classroom. Pascal's triangle can be generated with the use of a spreadsheet, but it is more common in the triangular form. Before going on to the triangular form, it is interesting to point out some of the patterns more easily seen in the rectangular array. The columns can be explored to yield the discovery that the fifth column is all multiples of 5 after the initial 1, and multiples of 7 in the seventh. A far more intriguing column is the third one where we can find a list of the triangular numbers. Drawings and discussions of triangular numbers would fit well here.


Students may use calculators to find this pattern and then calculate 11 to the fifth power. A question, "Why is this not row five?" might lead to interesting discussion. Another pattern to be explored is the sum of the rows. Seventh graders, with some coaxing with leading questions, can see the pattern of 1, 2, 4, 8, 16... as the powers of 2.


The patterns formed by divisibility rules on the numbers in Pascal's triangle result in interesting patterns, a possible motivator for the review of these rules. (Click here to see patterns formed by divisibility rules.)
While the amount of time spent on Pascal's triangle would be limited, the possibilities for relating many of the topics in number theory are great. The fact that 1 is neither prime, nor composite cannot be mentioned too often. Another easily forgotten math fact is that any number to the zero power is 1. This fact can be restated in this review at least twice. Factors and multiples in color might increase interest in a culminating lesson for a unit on number theory.
Click here for a illustration of Pascal's triangle with a spreadsheet using the mod function to create Sierpinski's Gaskets.