The students will be able to derive and use formulas for area and volume. The concepts presented here are sequential but they are not numbered nor labeled by day since the time spent may vary by class. Anchors are provided so that it is possible to go directly to the lesson plans for a specific concept.
Click herefor lesson plans on plane area, including squares, rectangles, parallelograms, triangles, trapezoids, and circles.
Click Herefor lesson plans on surface area, including prisms, pyramids, cylinders, and cones.
Click Here for lesson plans on volume, including prisms, pyramids, cylinders, and cones.
Math students in the seventh grade should have mastered the use of simple formulas as well as the use of all four operations with whole numbers, fractions and decimals. Before this unit they also should be proficient in the uses of inverses to solve mulit-step equations. The geometry chapter which includes vocabulary, and properties of quadrilateral, triangles, and three-dimensional figures is included in prior knowledge.
In order to use this unit, the classroom must be equipted with a computer, access to GSP, and an overhead projector connected to the computer. The students will need 1/4" grid paper on which to copy these constructions. A classroom set of calculators will enable the students to emphasize the derivation and use of formulas without spending undo time on the calculations.
In order to stress the concept of area, students will trace their hands on square centimeter grid paper and count the number of squares that their hands cover. The exercise needs to include how to handle partial squares. In order to strengthen the concept of square units, the students are asked to make a list of the smallest ten squares. A chart of the squares should reinforce the limitations on the possibilities of square figures and the formula A = n ^2.
Using the same grid paper as for the hands. students are asked to make as many figures as possible with a given area. Discussion of squares and rectangles, as to why they are the easiest figures to draw, need to include the concept of perpendiculars as well as the numbers of squares in each row times the number of rows. A spread sheet can demonstrate the relationship, and eliminating every outcome except integers will relate geometry to factoring in number theory.
At this point, students should be ready to use the standard formulas for the areas of squares and rectangles.
The first activity with the area of parallelograms is to compare the area to that of a rectangle. Each student is given a ruler and a large sheet of paper, 8 1/2 by 14". They are directed to find the area and perimeter of this sheet of paper, some students may even divide it with lines into square inches to count the squares.
Now the paper is torn diagonally within the long edges, with the students using the ruler or simply by repeated foldings. By exchanging parts, the students now have a parallelogram. They then compute the area and perimeter of this figure. When they finally realize that the area has not changed but the perimeter has, we can discuss the importance of the perpendicular distance.
The following sketchpad illustration can be put on the overhead to demonstrate the concepts involved in the new formula. (Click here for the GSP moveable sketch of parallelograms, from Key Curriculum Press.) The following construction shows the script with DF the perpendicular height in one position:
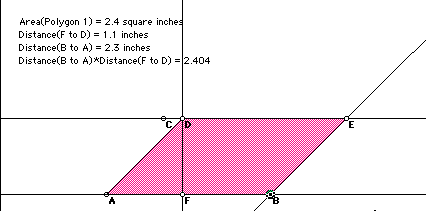
And the following diagram demonstrates the equal area but changed perimeter when DF is moved. The base and height, and therefore, the area remain the same.
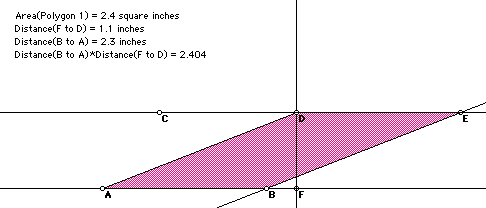
In order to reinforce the concept of A=bh, where b and h are perpendicular, we can show the example where DF is perpendicular to AB, and relate that to a rectangle.
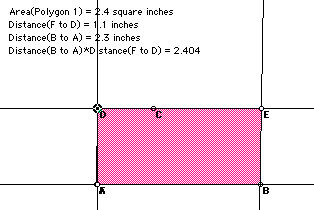
It is vital that we continue the concept of area with development of formulas rather than simply mechanical usage of them. The formulas for the area of a triangle can be developed as the area of half a parallelogram with the same base and height, or as one-half the height times the base.
The following diagram illustrates the half-height formula. The height AD is bisected, the top triangle formed is rotated 180 degrees at F to form a parallelogram with 1/2 height, and the same base.
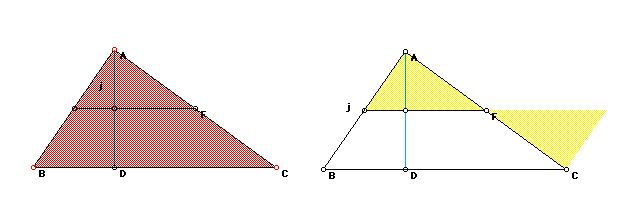
(Click here for a moveable GSP sketch with triangles, from Key Curriculum Press.) In the following diagrams, the triangle can be seen as 1/2 the area of the parallelogram formed with parallel lines constructed at the opposite vertices. It is easy to visualize that the area of the parallelogram is composed of two congruent triangles, therefore one triangle is half of the area of the parallelogram.
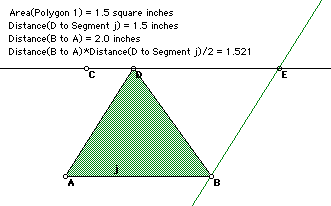
By moving D, the shape of the triangle is changed but the area does not because the base and the height remain constant.
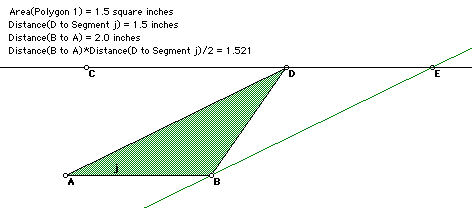
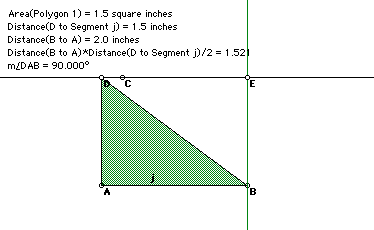
The right triangle is an example that illustrates all of the relationships between the formulas for rectangle, parallelogram and triangle.
The following day, we can develop formulas for trapezoids. (Click here for another moveable sketch, this one of a trapezoid, from Key Curriculum Press.)
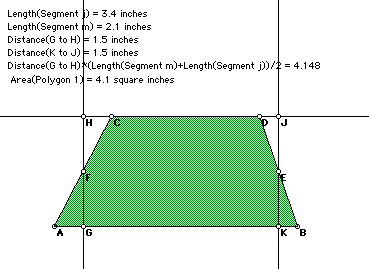
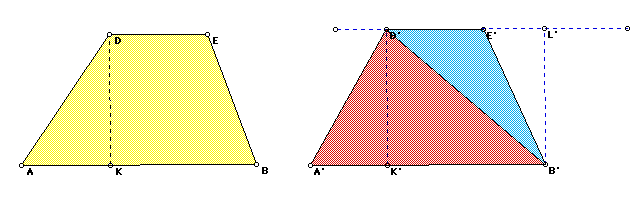
The following sketch can be used to demonstrate the algebraic derivation for the formula of the area of a trapezoid. The students can visualize the area of a trapezoid as the sum of the areas of the two triangles formed by a diagonal in the given trapezoid. It must be pointed out that because the bases of the trapezoid are parallel, therefore the height is the same for both triangles. The students are capable of following the following algebra, where h is the perpendicular distance between the bases, and a and b are the bases of the trapezoid.
First write a formula for the sum of the triangles:
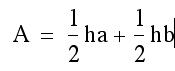
The students can explain that the distributive property is used to rewrite the formula as a product rather than a sum.
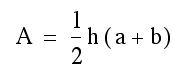
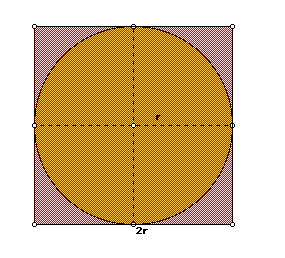
The following construction demonstrates the relationship between the area of a square with side of 2r or d, to a circle with radius r. While this is not formal, the students can see that each quadrant is a square with area of r squared. This makes the entire square 4 times r squared. In order to take into account the pink corners, the circle must be less, or 3.14 times r squared.
A less intuitive approach to the area of a circle is the demonstration shown in the following three diagrams. The circle is sectioned into wedges by diameters every 20 degrees. If these wedges are then reorganized with the top half pointing down and the bottom half pointing up to fill in the gaps, they form a parallelogram with perpendicular height of radius length and base of 1/2 circumference.
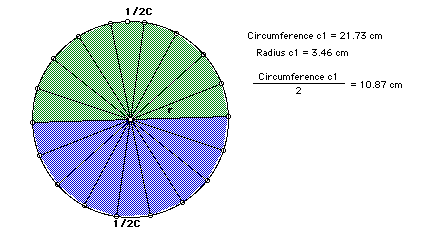
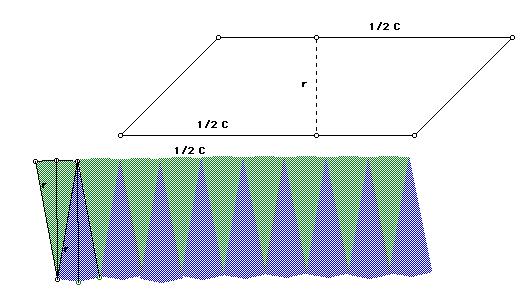
The algebra that accompanies these illustrations if difficult for some students but needs to be included in the derivation of the formulas. The area of the parallelogram is base, 1/2 circumference, times height, radius.
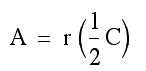
Now we replace C with pi times diameter:
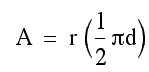
And replace d with 2r:
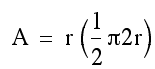
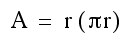
At this point of the unit, students need to apply these skills to solve problems of combined figures, such as a circle inscribed in a square, or a triangle combined with a rectangle. Such problems should reinforce this plane area understanding and prepare the students to think of the combination areas in surface area of three-dimensional figures.
Surface area is one of the most difficult concepts for middle school students because of the problem of visualizing a three-dimensional object in a two-dimensional drawing. Therefore hands-on activities of building these figures out of paper nets will be included in the lessons.
The surface area of prisms is limited to right prisms, in the seventh grade both rectangular and triangular. Other prisms can be explored, the students can find the lateral surface area of pentagonal, hexagonal and even octagonal prisms, and total surface area if given assistance in finding the area of the bases. The first step is to find the congruent faces of the prisms which involves visualizing the three-dimensional figure in a two-dimensional space.
The easiest of these being the cube. It is advantageous to compute the surface area in two different but ralated methods. It can be seen as the sum of the areas of the six faces, each face being a square with area computed by A=s squared. This can be put into a table to see each computation.

An alternate method is to develop a formula for the surface as a summation of the areas of the faces. This conceptualizing will be used repeatedly in the more difficult surface area problems.
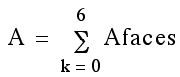
The advantage of this method is the ease of solving. Using the previous example, we get:
The net gives a visual aid for the students to see the six squares, where the area of each is calculated by squaring a side, then all six are added.
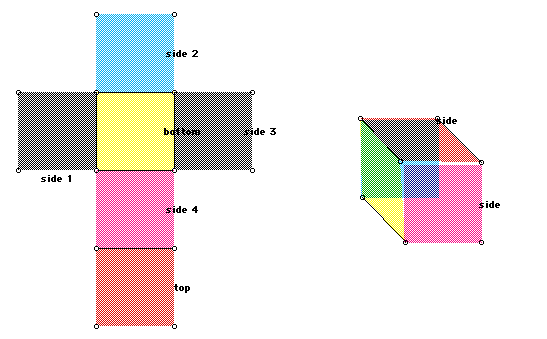
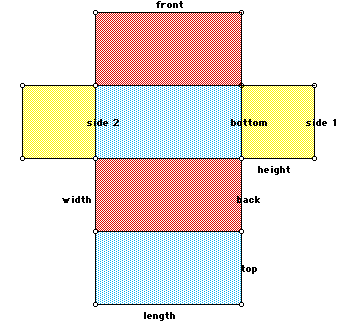
Rectangular prisms present more difficulties in recognizing faces and dimensions. The drawing of the prism flattened should allow the students to see that the length along the front must be the same for the back, and the bottom and the top. Finding the widths is easier also when the students can see the net, in this example the width of the back is the same as the height of the sides. Again they could use a table with six sides, each a rectangle with A=lw, then add all of the areas. Some students would prefer one formula to do the surface area at once. They can help derive:
It as this point that the greatest difficulties occur, which dimensions on the drawing are the lengths and widths since each number in the diagram is used twice in the formula.
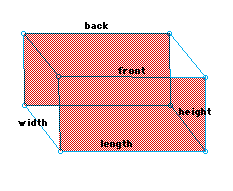
The triangular prism creates the same difficulties in recognizing faces, and using dimensions in the appropriate formulas. Again the students can make a table, this one having only five faces, 2 triangles and 3 rectangles. They need to recognize that each rectangle has the same height, the distance between the bases, but each can have a different width depending on the sides of the triangles. It is also important for them to find the base and perpendicular distance inside the triangle in order to calculate the area of the bases. The class can also derive a single formula to find this surface area:
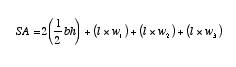
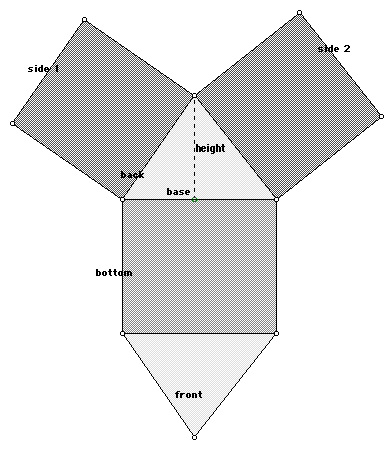
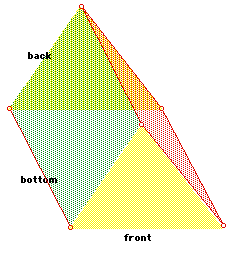
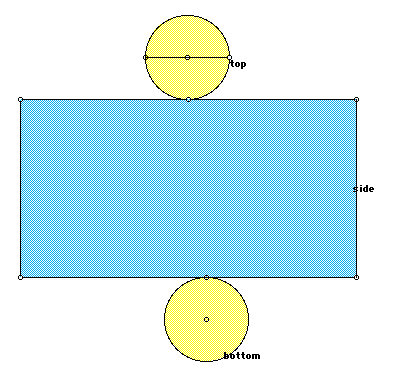
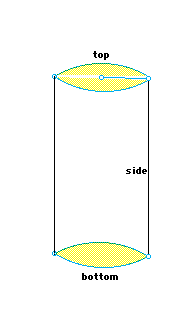
While the surface area of a cylinder appears to be more difficult, it does not involve so many options and therefore is much simpler to calculate. The table would be made of only three areas, two circles and a rectangle between them. To review the formula for the area of a circle, we repeat:
And the area for the rectangle must go around the circle, so it has length equal to the circumference of the circle, and height is the distance between the bases. The resulting equations for the side are therefore:
![]() and rewritten using r becomes
:
and rewritten using r becomes
:![]()
We can also develop a single formula for the surface area:
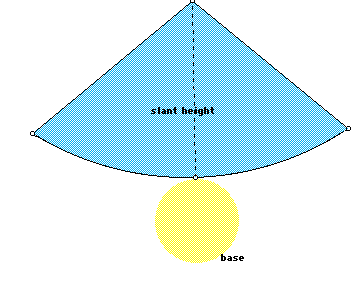
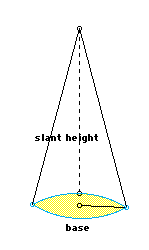
These students are not likely to be able to find the area of the surved section forming the side of the cone, but they can relate it to the shape of a triangle, so the area formula can be explained as simply 1/2 of the surface area of a cylinder with the same radius and height, because it has only one circle and a triangular-type shape. We derive the formula:
It is now that students need to be made aware of the two different heights of cones, the slant height measured along the face from the vertex to the circumference of the base, and the height of cone, the perpendicular distance from the vertex to the center of the circle at the base.
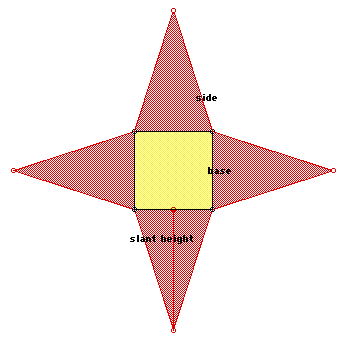
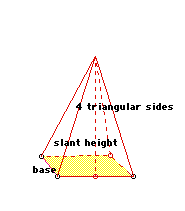
The surface area of pyramids simply reinforces the previous surface area concepts. Again, the students can choose to use a chart or develop a single formula. They need to be aware that the triangular lateral faces require slant height as do the cones, and that the formula is A=1/2bh.
Surface area is an opportunity for the teacher to encourage students to understand concepts, think logically, and solve multistep problems. It may require a step-by-step process for instructions to begin, however, the students should be able to do more and more of the reasoning to develop the formulas.
Volume is best explained as filling up an object. The general formula for prisms and cylinders can be given as:
where B is the area of the base and h is the height of the object. Another general formula is used for cones and pyramids for the same B and h:
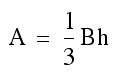
The easiest volume is that of a cube or rectangular prism. The students may recall from previous grades that V=lwh. Relating that formula to V=Bh, the students should be able to relate area and volume, two-dimensional measures to three-dimensional.
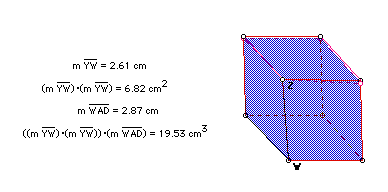
Click Here to see the diagram above in which you can change the height of the volume in the cube.
Volume of a cylinder follows the same development, where B=area of the circular base. The student should also derive the following formula from that understanding:
A triangular prism gives students trouble when not sitting on one triangular bases, they often confuse this figure with a pyramid. Therefore, they need to practice computing area of a prism pictured in either position.
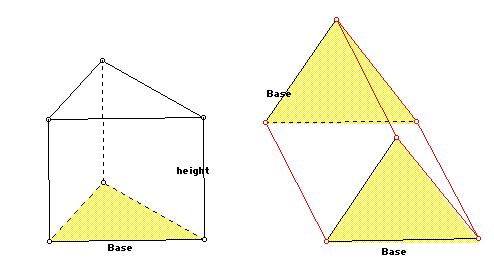
The most fun is having students relate the volume of a pyramid to that of a prism with the equal base and height, and a cone to that of a cylinder with equal base and height. With a bucket of blue water and clear plastic models of the four figures, we can guess the relationship before pouring water from one model into the other.

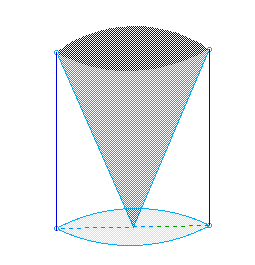
The possibiliities for using technology in a seventh grade geometry class are available to enrich the learning of each student. Manipulatives for area with paper, for surface area with paper nets, and for volume with models also increases student engagement. It is a difficult unit for students to master, but one of the most interesting to teach.