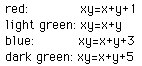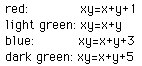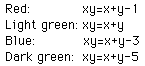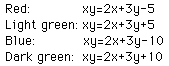EMT 668
Final Project I
by
Beth Richichi
Consider graphs of the equation xy=ax+by+c.
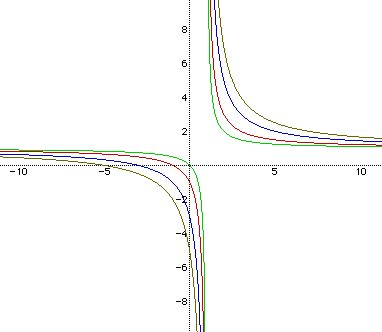
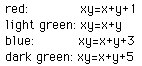
The values of a and b are held fixed at 1. The value of c is greater
than or equal to zero. Here we have a set of hyperbolas with the horizontal
asymptote at y=1 and the vertical asymptote at x=1.
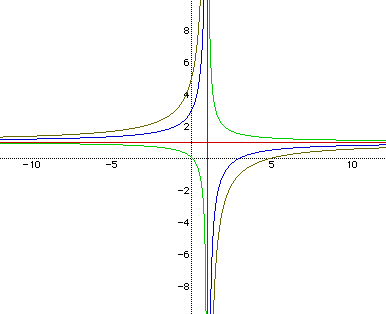
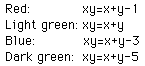
Here the values of c are less than or equal to zero. When the value of
c is negative, the hyperbolas "reverse" in direction. The asymptotes
remain the same as those of the previous graph. Notice that when c=-1 (the
red curve) we see asymptotes intead of hyperbolas which intersect the axes
at x=1 and y=1. Notice that the larger value of c moves the curve further
away from each asymptote.
An examination of the above curves illustrates the "job" of
the c value. The c value determines the location of the hyperbola in terms
of quadrant placement and distance from the asymptotes.
This time let's hold the values of a and b fixed, yet let a and b be
different values.
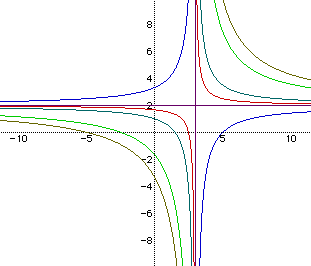
Let's examine the equations of x-b=0 and y-a=0 with an a value of 2 and
a b value of 3. The equations x-3=0 and y-2=0 yield asymptotes at x=3 and
y=2. Multiplying these two equations,
- (x-3)(y-2)=0
- xy-2x-3y+6=0
- xy=2x+3y-6
Aha! This is the equation corresponding with the purple curve above!
Thus, from the equation (x-a)(y-b)=0, we can see that we will find the horizontal
asymptote at y=a and the vertical asymptote at x=b. When (x-a)(y-b) is not
equal to 0, we have the equation (x-a)(y-b)=k for some value of k not equal
to 0. As demonstrated above, this equation will result in a the graph of
a family of curves, or more specifically, a family of hyperbolas.
To return to Beth Richichi's homepage, click here.