EMT 668
Final Project III
by
Beth Richichi

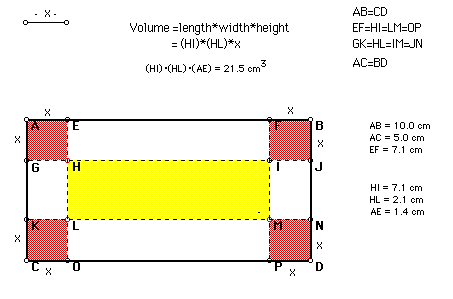
If given a rectangular sheet of cardboard and a small square of the same size cut from each corner, while each side folds up to form a lidless box, explore what sizes of squares can be cut from each corner to produce a box with a certain volume. Explore what sizes of the square produce the maximum volume.

We can explore this problem using different methods. First, let's examine this problem by way of GSP:

I have chosen the length of the box to be 10 cm. and the width of the box to be 5 cm. for the purpose of simple illustration. Let the height of the box be x cm. As the length of x varies, the box will also vary. Click here to view this GSP illustration.

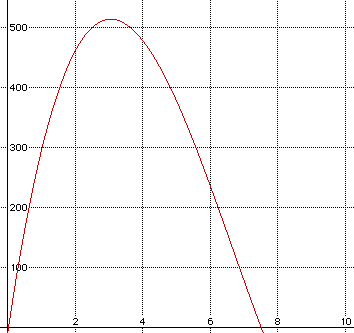
Now let's assume the rectangular sheet of cardboard is 15 x 25 inches. Let's explore what size squares may be cut from each corner to produce a volume of 400 cubic inches and what size squares are necessary to produce a maximum volume. To do this, let's use the equation
x(15-2x)(25-2x), where x is length of the square to be cut from each corner.

The volume is seen along the y axis, while the length of x is seen along the x axis. Notice that the maximum of the graph is at appromately x=3 and that the volume is 400 at approximate values of x=1.55 and x=4.8.

Using spreadsheets, one can explore variations of the value of x and of the volume of our lidless box with the corresponding x value.


The volume of 400 cubic inches is found when x is approximately 1.525



Again, we see that the volume of 400 cubic inches is found when x is approximately 4.792.

As seen in the graph constructed above, we also see that the volume is 400 cubic inches when x is two different values: approximately 1.55 and 4.8.


Again corresponding with the graph above, the maximum volume is found when x is approximately 3.06.

To return to Beth Richichi's homepage, click here.