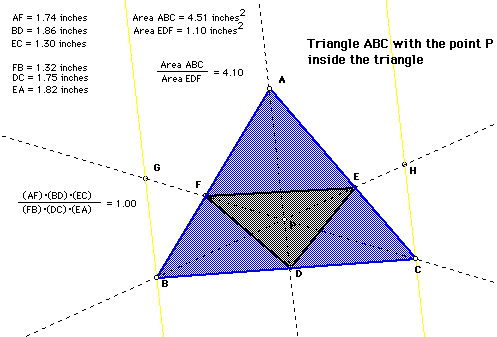
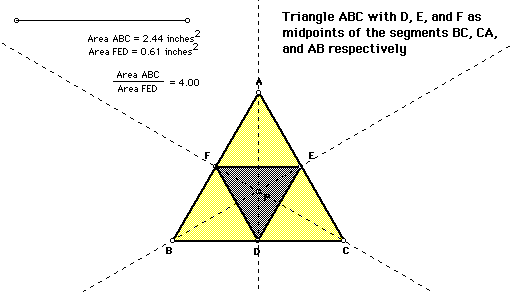
Consider the triangle ABC. The point P has been selected inside of the
triangle. The lines AD, BE, and CF have been constructed so that they all
are incident with the point P and that they each have been extended to their
intersections with the opposite sides in points D, E, and F respectively.

Move the point P to different locations inside the triangle ABC. To do
this, view the GSP construction by clicking here.
Notice that as P is moved to various locations inside the triangle, the
ratio of (AF*BD*EC) to (FB*DC*EA) will always be equal to one.
To prove this, let's examine several equivalence relations:
We see that ![]() and
and ![]() since Triangle
PBD is similar to Triangle HBC and Triangle PCD is similar to Triangle GCB.
Since Triangle GFB is similar to Triangle PFA and Triangle HEC is similar
to Triangle PEA,
since Triangle
PBD is similar to Triangle HBC and Triangle PCD is similar to Triangle GCB.
Since Triangle GFB is similar to Triangle PFA and Triangle HEC is similar
to Triangle PEA, ![]() and
and ![]() . From looking at the similar triangles, we
see that
. From looking at the similar triangles, we
see that ![]() ,
, ![]() ,
,![]() , and
, and ![]() .
.
From the first two ratios, ![]() . Thus,
. Thus, ![]() .
.
Hence ![]() . QED.
. QED.
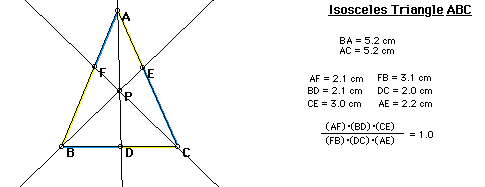
To view the GSP construction of the isosceles triangle, click here.
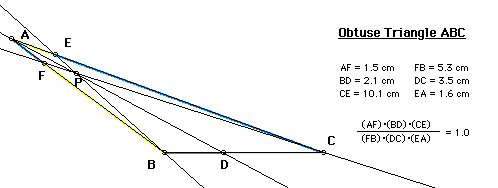
To view the GSP construction of the obtuse triangle, click here.
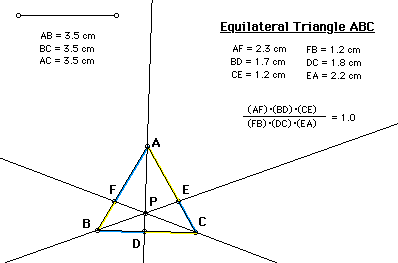
To see the GSP construction of this, click here.
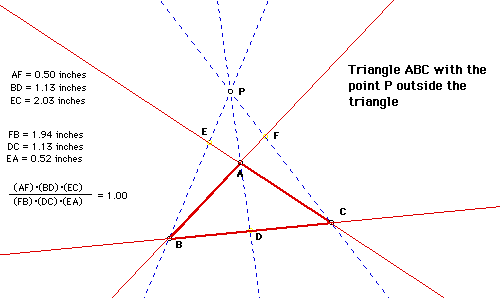
Move the point P to different locations outside the triangle ABC. To
do this, view the GSP construction by clicking here.