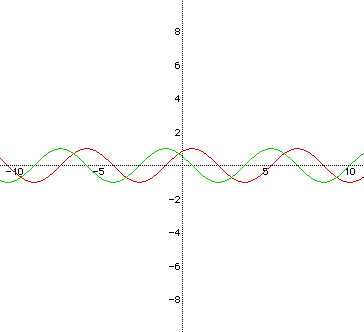
Let f(x)=a sin(bx+c) and g(x)=a cos(bx+c). For selected values of a,
b, and c, graph and explore:
First let's examine the following graphs where a, b, and c have values
of one. The red graph has the equation f(x) = sin(x+1). The green graph
has the equation g(x)=cos(x+1).

Let's examine the results when we perform operations on the two functions:
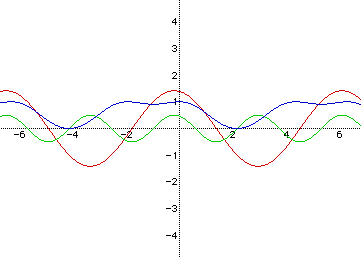
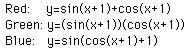
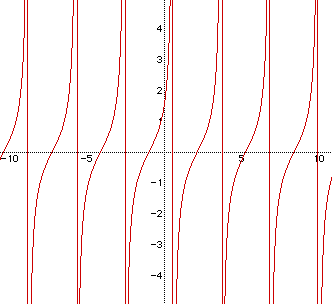
When a and b have positive values and c is equal to zero, the result
will be the following:
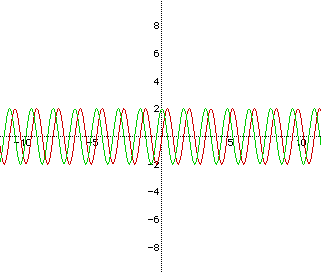
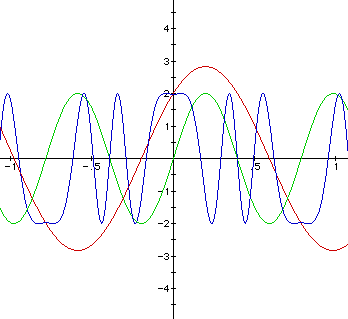
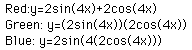
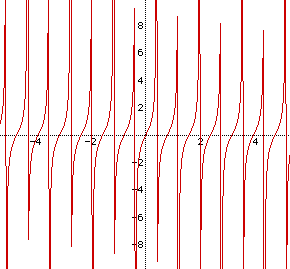
After exploration with WriteUp I, I have seen that the value of a alters
the amplitude of the graph; the value of b alters the periodicity of the
graph; and the value of c shifts the graph either to the left or to the
right. It is valuable for students to also examine operations on the functions
in order to view how these operations again, alter the graphs, thus changing
the amplitude, periodicity and location of origin.