y = sin x

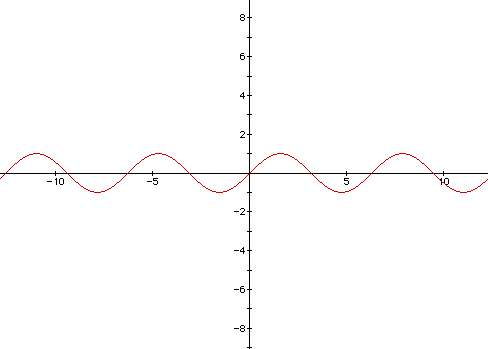
The graph of y = sin x intersects the x axis and y axis at the origin. The maximum and minimum are at y = 1 and y = -1, respectively. Each period has a length of 2pi. The maximums are at x = pi/2, x = (5pi)/2, and so on. The minimums are at (3pi)/2, (7pi)/2, and so on. There is an alternating maximum or minimum every distance of pi, starting at x= pi/2. Since the graph of the sine function is symmetric with respect to the origin, sin(-x) = -sin x. Note that since there are 2pi radians in one complete revolution, it follows that sin x = sin(x + 2pi). This idea will be further illustrated in later graphs.

y = 5 sin x

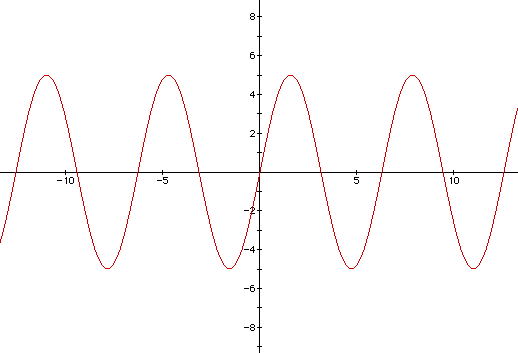
To obtain the graph of 5sin x, we multiply the y coordinate of each point on the graph of sin x by 5. The maximum and minimum are y = 5 and y = -5. The period continues to have a length of 2pi. Again, every distance of pi there is an alternating maximum or minimum.

y = -5 sin x

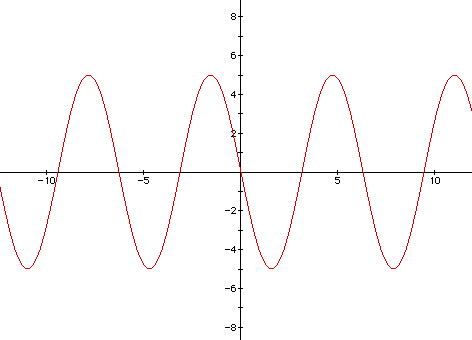
Since sin (-x) = -sin x, to obtain the graph of -5sin x, we reflect the graph of 5sin x through the x axis. Therefore, to obtain the graph of sin bx when b<0, the graph of sin |b|x is constructed and then reflected through the x axis. The period is 2pi/ |b|, or in this case, 2pi/ |-5 | = (2/5)pi.

y = 1/3 sin x

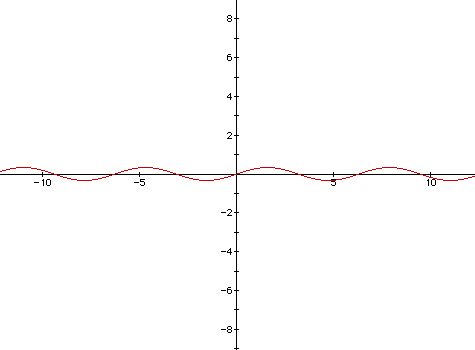
To obtain the graph of (1/3)sin x, we multiply the y coordinate of each point on the graph of sin x by 1/3. Hence, the value of a in the equation y = a sin (bx + c) increases or decreases the amplitude of each period.

y = sin 5x

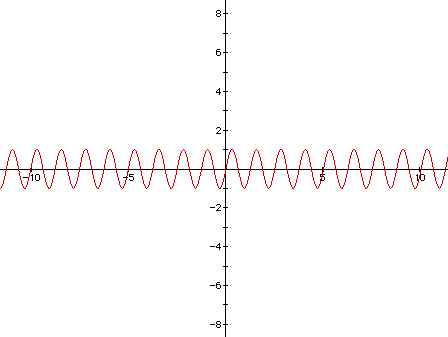
In this case, b=5. This function is periodic and its values are repeated every (2pi)/5 units. Hence, sin 5(x + (2pi)/5) = sin(5x + 2pi) = sin 5x. The graph of sin 5x is determined by its graph on [0,(2pi)/5]. Comparing the graphs of sin bx and sin x, we see that if b >1, then the graph of sin x must be contracted horizontally to obtain the graph of sin bx, whereas if 0< b< 1, then the graph of sin x must be expanded horizontally to obtain the graph of sin bx. In either case the graph is contained in the region between the horizontal lines y= -1 and y=1. The case where b<0 will now be discussed.

y = sin (-5x)

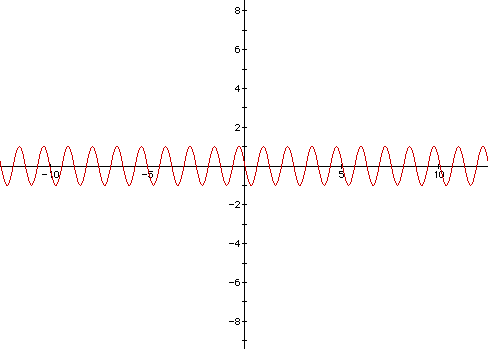
It is easier to examine the effect of a negative b value after examining a similar graph with a positive b value. Comparison of the graphs of sin 5x and sin -5x illustrates a mere reflection in the graph through the x axis.

y = sin (1/2)x

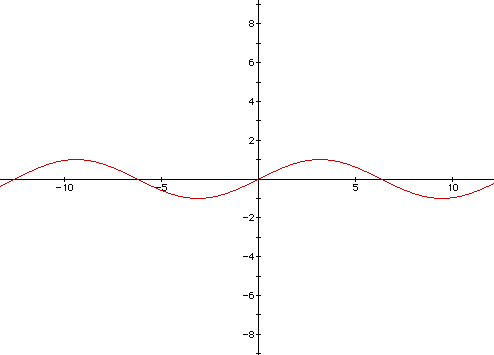
Here, b=1/2, so the period is (2pi)/(1/2) = 4pi. It follows that the graph of sin (1/2)x is obtained by expanding the graph
of sin x horizontally. Thus, the value of b in the equation y = a sin (bx + c) alters the periodicity.

y = sin (x + 1)

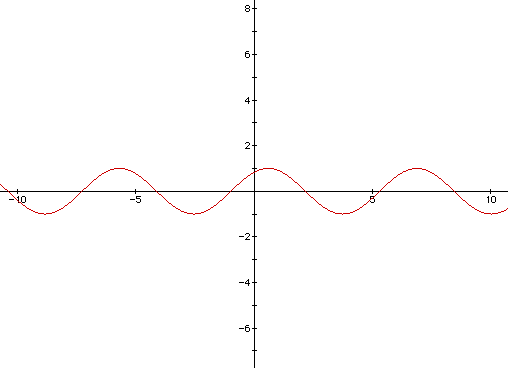
The graph of sin b(x+c) is the graph of sin bx shifted to the left c units if c>0, and the the right c units if c<0. In general, sin b(x+c) and sin bx have the same period.

y = sin (x - 5)

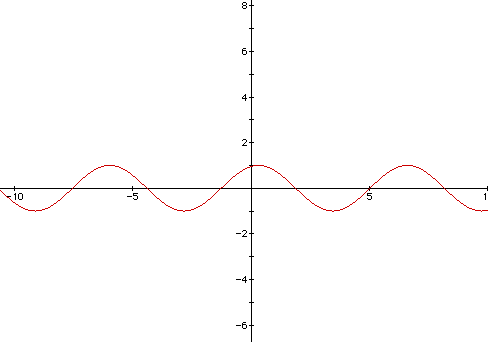
To obtain the graph of sin (x-5), the graph of sin x is shifted to the right 5 units since (c=5) > 0. The point of origin has been shifted to (5,0).

y = sin (x - 4/5)

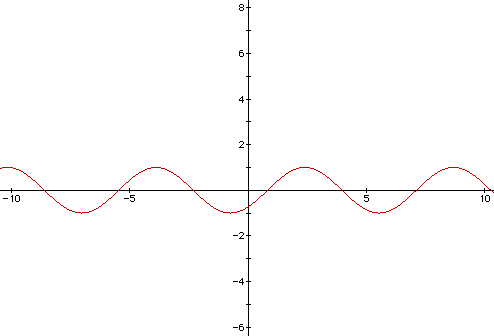
Here is another example of the graph of sin x being shifted to the right. In this case, the graph is shifted c=4/5 units to the right.

y = -2 + 4sin(2x + 1/2)

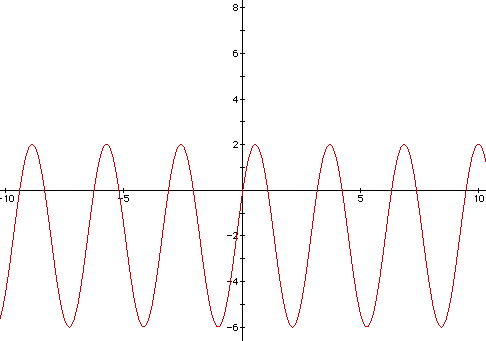
Here we have a combination of a change in the a, b, and c values for the equation y = a sin (bx + c). In comparison with the graph of sin x, the value of a increases the amplitude by 4. Since b>1, the graph of sin x is contracted horizontally when b=2. A c value of 4 shifts the graph of sin x 4 units to the left. The -2 at the beginning of the equation shifts the entire graph down 2 units.

In conclusion, the values of a, b, and c of the equation y = a sin (bx + c), alter the graph in various ways. The a value alters the amplitude of the graph; the b value alters the periodicity of the graph; and the c value shifts the graph to the right or to the left along the x-axis, depending on its negative or positive value.