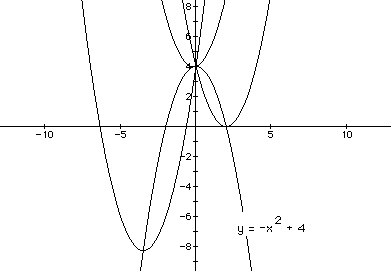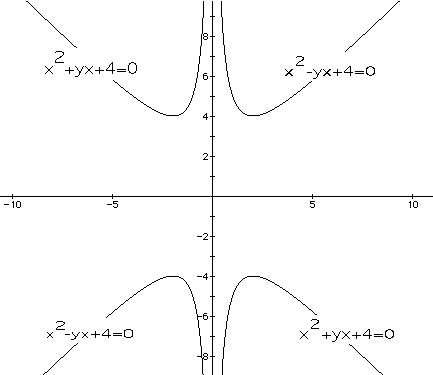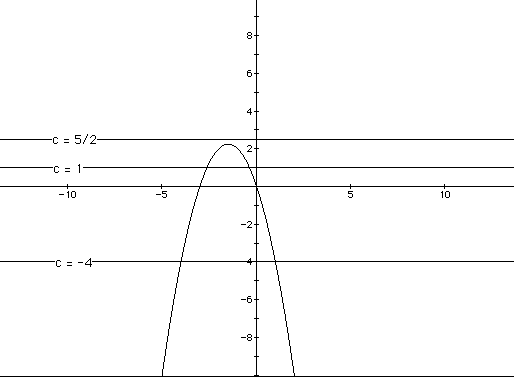Write-up II
EMT 668
Some different ways to examine
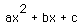
by
James W. Wilson, Brian Seitz and Beth Richichi
It has now become a rather standard exercise, with available
technology, to construct graphs to consider the equation
.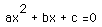
For example, let's give values to the a,b, and c variables and
examine the graph of the following equation, where a=1, b=2, and c= -3:
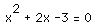
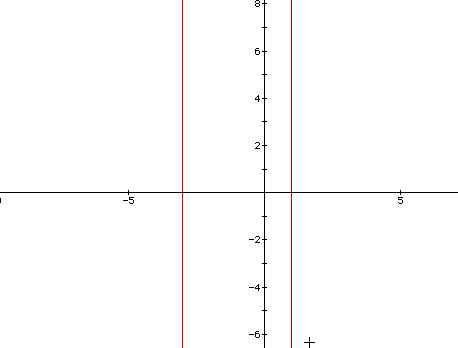
Here, the lines are parallel to the y axis and intersect the x axis at x=
-3 and x= 1.
The graph of a quadratic equation is a parabola.
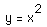
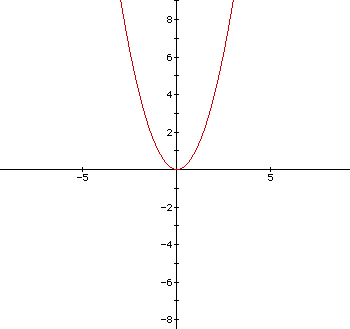
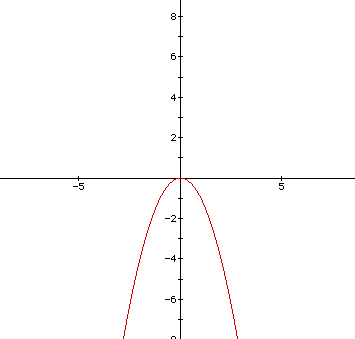
Notice that the graph of  opens upward,
whereas the graph of
opens upward,
whereas the graph of 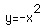
opens downward.
Now, let's examine the graph of 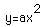
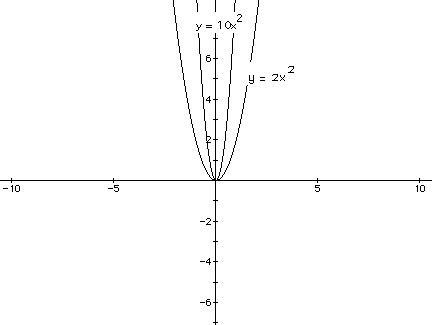
Notice that the y coordinate of each point on the graph is twice the y coordinate
of the corresponding point on the graph of
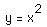 .
.
Here, we have the same graph with a negative value of a:
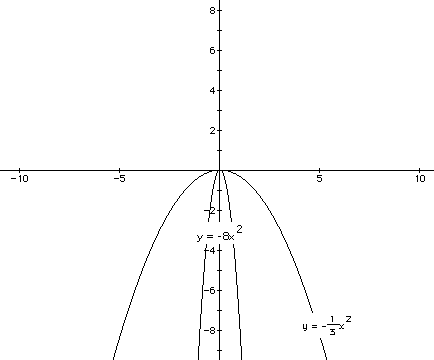
Here, the y coordinate of each point on the graph is 1/3 the y coordinate
of the corrsesponding point on the graph of 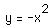 .
.
If 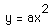 with a not equal to 0, then the graph has the
same general shapes as that of
with a not equal to 0, then the graph has the
same general shapes as that of 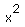 or
or 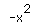 depending on whether
a>0 or a<0. The graph, however, is more wide if |a|<1 and is more
narrow if |a|>1. In either case the graph is symmetric with respect to
the y axis. The origin is the maximum if a<0 and the minimum if a>0.
depending on whether
a>0 or a<0. The graph, however, is more wide if |a|<1 and is more
narrow if |a|>1. In either case the graph is symmetric with respect to
the y axis. The origin is the maximum if a<0 and the minimum if a>0.
Let's examine the following quadratic equation:
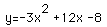
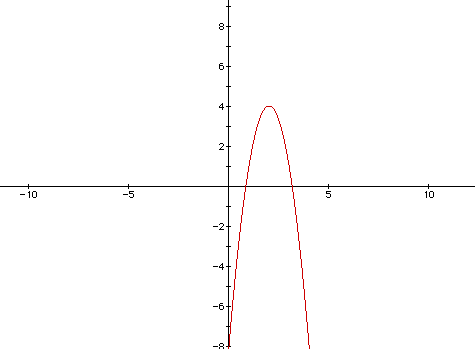
The use of today's technology is of great help when examining correct
solutions to the quadratic formula and the method of completing the square.
When x=0, we see that y=-8, so the y intercept is -8. When y=0, the quadratic
formula helps us to see that the x intercepts are x=2-(2/3)rt(3), x=2+(2/3)rt(3).
Completing the square, we find that 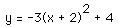 From this we know that the
vertex of the parabola is (2,4). Thus we obtain the graph of the given equation
by shifting the graph of
From this we know that the
vertex of the parabola is (2,4). Thus we obtain the graph of the given equation
by shifting the graph of 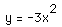 upward 4 units and to the right 2 units.
The use of today's technological methods, such as Algebra Xpresser, allows
students to easily check their work.
upward 4 units and to the right 2 units.
The use of today's technological methods, such as Algebra Xpresser, allows
students to easily check their work.
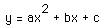
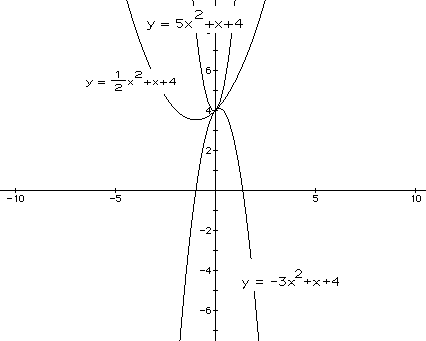
We see varied values of a in the above graphs: a= 5, a=1/2, and a= -3.
A negative value of a turns the parabola upside down with respect to the
x-axis. As the value of a increases, the width of the parabola becomes more
narrow. Similarly, a decrease in the value of a widens the parabola. The
three parabolas meet at the point of locus, (0,4).
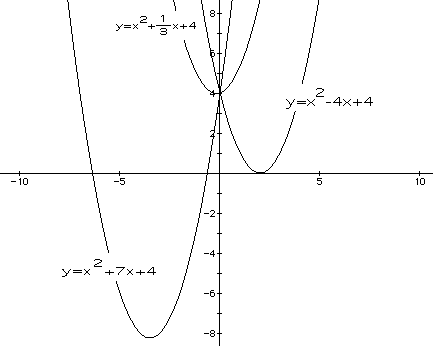
Here, the b value has been altered. A negative value of b shifts the parabola
to the right of the y axis. Similarly, a positive value of b shifts the
parabola to the left of the y-axis.
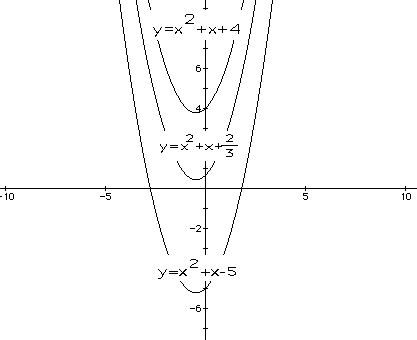
Alteration of the c value shifts the parabola up and down the y-axis.
The width of the parabola remains the same. The parabola will intersect
the y-axis at the value of c. For example, when c=-5, the parabola intersects
the y-axis at (0,-5).
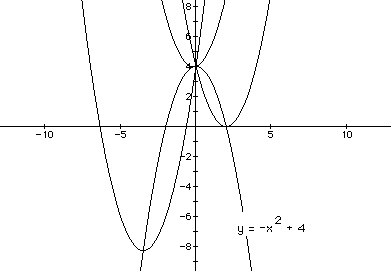
Since the three parabolas meet at (0,4), the locus is the parabola 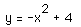 .
.
Now let's examine 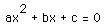 for different values of a, b, or
c as the other two are held constant. For example, if we vary the value
of b while a and c are held constant by setting
for different values of a, b, or
c as the other two are held constant. For example, if we vary the value
of b while a and c are held constant by setting 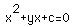 , the result
would be the following graph:
, the result
would be the following graph:
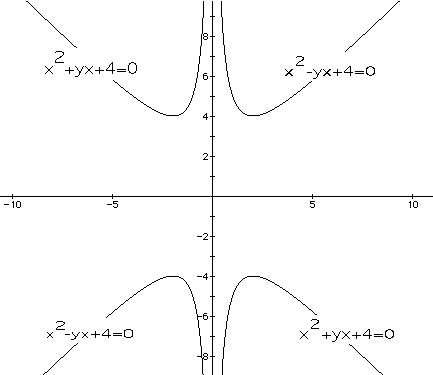
A positive value of b places the parabolas in quadrants II and IV. A negative
value of b places each parabola in quadrants I and III. These graphs are
inverses of each other and do not lie between y=-4 and y=4.
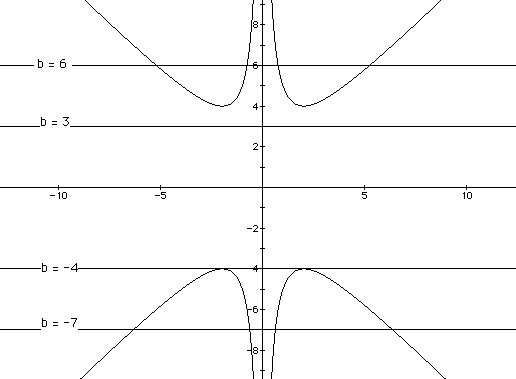
Setting values of b=-7, b=-4, b=3, and b=6 results in horizontal lines
parallel to the x-axis. The lines b=-7 and b=6 intersect each parabola at
two distinct points. The line b=-4 intersects each parabola at only one
poiint, the maximum. The line b=3 does not intersect the parabola, since
this line lies between y=-4 and y=4. From this we can determine that for
b>4, the result will be two negative real roots. Similarly, for b<-4,
the result will be two positive real roots. For b =-4 , the result will
be one real root. For -4<b<4, there will be no real roots.
Similarly, the a and b values may be held constant while the
c value varies. For example, let's examine the graph of 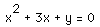 :
:
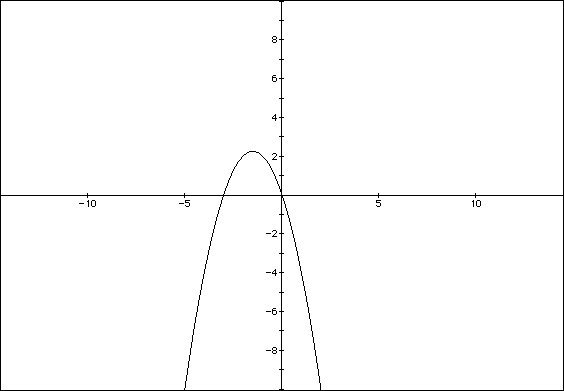
Here, we have a graph in the xc plane, where a and b are held constant while
c varies.
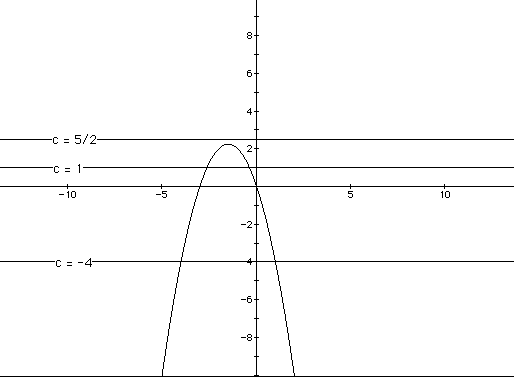
Notice that the c intercepts intersect the parabola at two points, except
for the maximum, where the c intercept intersects the graph at one point.
The value of a can also be altered. Let's examine 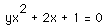 :
:
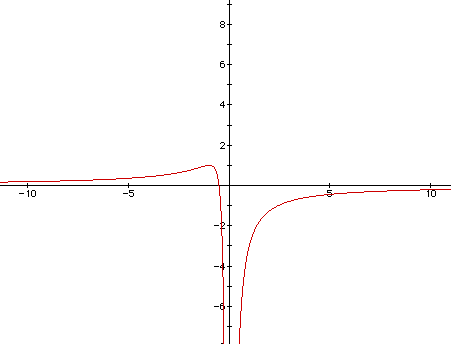
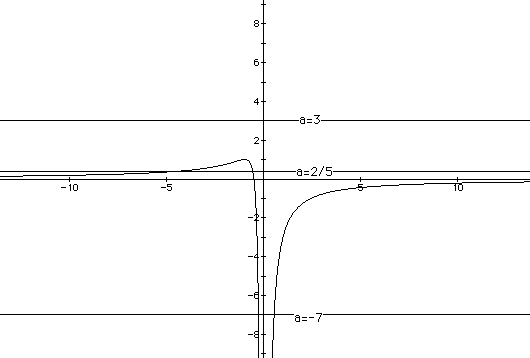
We see that the a-intercepts intersect the parabola at 0 or more points.
Back to Beth
Richichi's homepage
Back to Brian
Seitz's homepage





![]() From this we know that the
vertex of the parabola is (2,4). Thus we obtain the graph of the given equation
by shifting the graph of
From this we know that the
vertex of the parabola is (2,4). Thus we obtain the graph of the given equation
by shifting the graph of ![]() upward 4 units and to the right 2 units.
The use of today's technological methods, such as Algebra Xpresser, allows
students to easily check their work.
upward 4 units and to the right 2 units.
The use of today's technological methods, such as Algebra Xpresser, allows
students to easily check their work.