EMT 668
Write-up IV
An Investigation of r=a+bcos(kt)
by
Beth Richichi and Brian Seitz

The graph of an equation of the form r=a (+ or -) bcost or r=a (+ or -) bsint is a limacon. If b>a, the limacon has a loop. If a=b, the limacon is a cardioid. If a>b, the limacon has a shape which appears as if it is a circle with an indentation.

Let us consider the above equation when a=b and k=1:

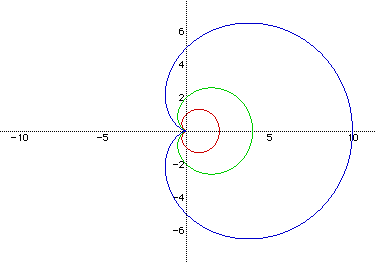
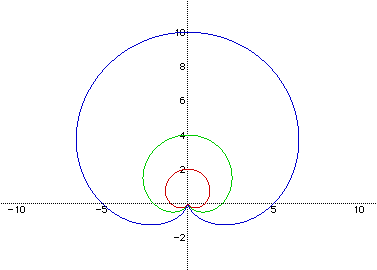
Three graphs have been constructed above. The red cardioid has the equation r=1+cos(t). The green cardioid has the equation r=2+2cos(t). The blue cardioid has the equation r=5+5cos(t). Notice that the graph is symmetric with the x axis.

Notice that for the same values of a,b, and k, for the sine graph, the cardioid has been rotated ninety degrees and is now symmetric with the y axis.



Now, keeping the value of k equal to 1, let's see what happens when a<b:


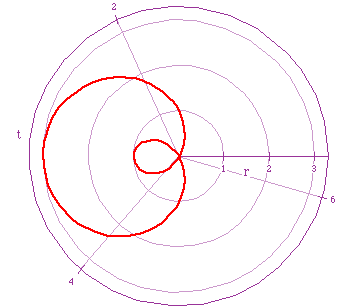
Red Limacon: r=1-2cos(t)


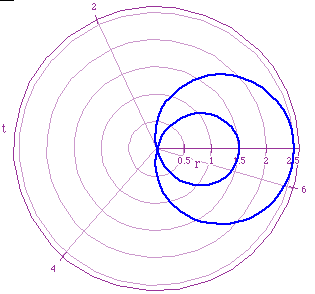
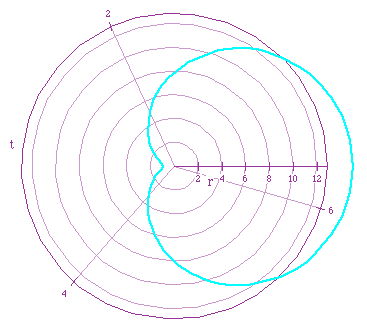
Again, holding k=1, let's see the graphs when a>b:


Cyan Limacon: r=8+7cos(t)


Lilac limacon: r=3+2sin(t)

Many textbooks stress the "n-leaf rose". Let's explore this rose first holding a equal to 0 as n=k and k varies.

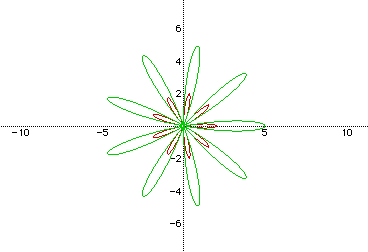
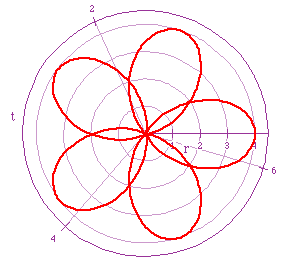
Here, the green "rose" has the equation r=5cos(9t). Notice that there are 9 "leaves" of the green rose and that when b=5, the graph is located between values of x=-5 and x=5. The red rose has the equation r=2cos(9t). Again, there are k=9 leaves of the rose, but this time, the graph lies between x=-2 and x=2.

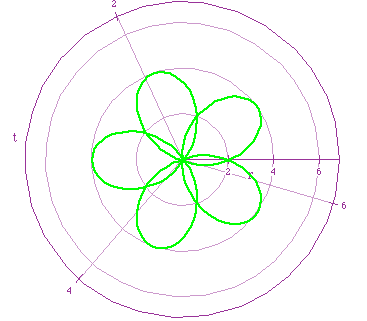
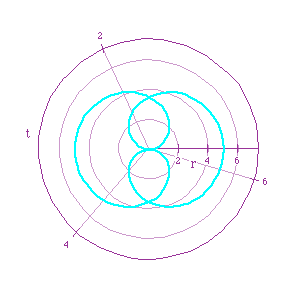
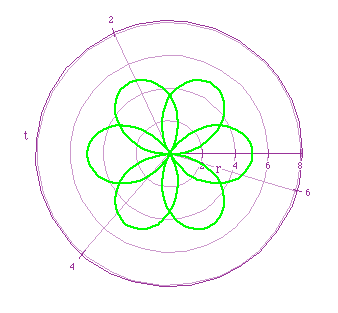
Let's examine this n-leaf rose when a and b are equal. Here, we shall examine rational values of k while t varies over [0,4pi].






Green: r=5cos(3t/2)

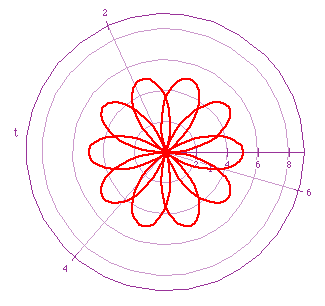
Red : r=5cos(5t/2)
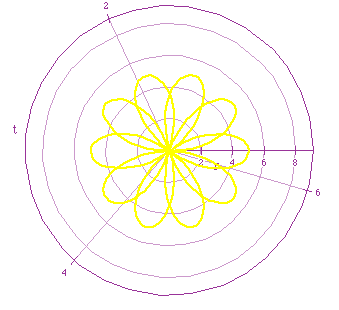
Keeping the same values for a, b, and k, let's view the sine graph:

Yellow: r=5sin(5t/2)

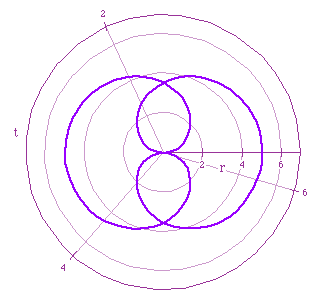
Purple: r=5sin(t/2)

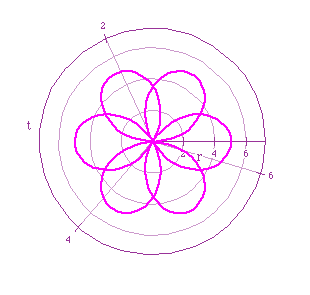
Magenta: r=5sin(3t/2)
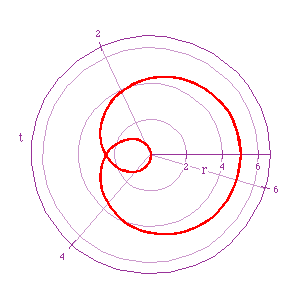
Here, we shall examine other rational values of k while t varies over [0,6pi].

Red: r=5cos(t/3)

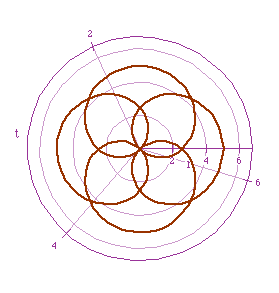
Brown: r=5cos(2t/3)

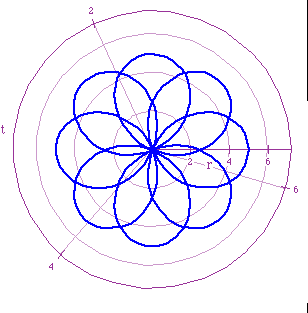
Blue: r=5cos(4t/3)
Again we see that the k value alters the number of leaves on the rose, while the b value determines the span of the curves along the x and y axes.

Keeping the same values for a, b, and k, let's view the sine graph:

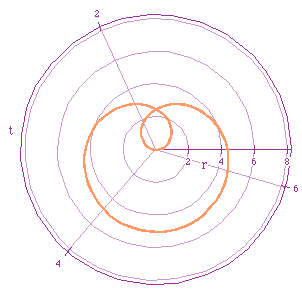
Camel: r=5sin(t/3)


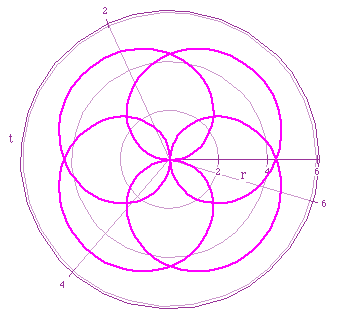
Magenta: r=5sin(2t/3)

Green: r=5sin(4t/3)
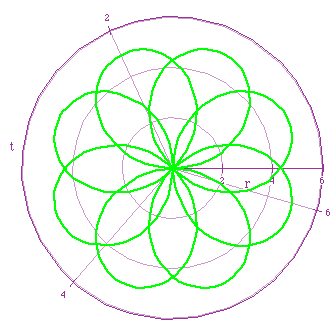
A variation of the k value changes the number of leaves on the rose when a and b are equal and k is an integer. A change in the values of a and b results in a change of the sizes of the leaves of the rose, how far the rose spans along the x and y axes (this is further illustrated below), and the location of the leaves on the rose with respect to the origin. When k is not an integer, let k=x/y. In these cases, as seen above, there are y sets of roses.
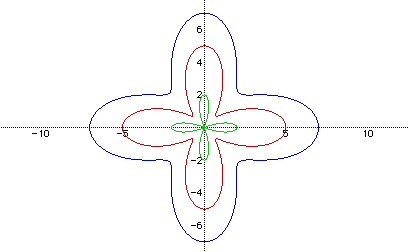
Let's vary the b and k values again, but this time let's try it with values of a>0:

Green rose: r=2cos(4t)
Red rose: r=3+2cos(4t)
Blue rose: r=5+2cos(4t)
Whereas the green rose spanned to x and y values of -2 and 2, the red rose spans from x,y =-5 to 5 and the blue rose spans from x,y=-7 to 7. Notice that the value of a stretches the graph a units from the original equation.

Keeping the same values of a, b, and k for the sine graph shifts the green, red, and blue roses so that they are no longer symmetric to the y axis, but symmetric to the origin:
Back to Beth Richichi's homepage
Back to Brian Seitz's homepage