Different Ways to Investigate Conic Sections

by
Jennifer Roth

I would like to discuss why I chose to do this essay before I get started on the topic. I have to admit that I need to learn much more about this topic before I feel comfortable teaching it, so this is really an investigation so I can learn more about the topic. I think it is also an exciting idea for and entire class to have access to the software that we have available to us. There would be so many materials available to use in teaching these topics to our students. The following unit plan includes using the different software that we have available to us.
Conic sections are the curves formed when a plane intersects the surface of a right cylindrical cone.
The general equation for a Conic Section is .
These curves are the circle, ellipse, hyperbola, and the parabola. For a circle A=C; for a parabola either A or C is zero; for an ellipse A and C have the same sign, and A is not equal to C; for an hyberbola A and C have opposite signs.
I am going to look at each of these 4 conic sections separately.

First, we will review what we know about circles.

Circles

The equation of a circle can be derived from the distance formula. If we have a circle with center (h,k) and radius r as follows

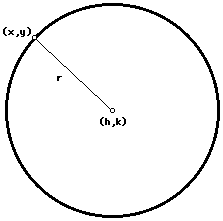
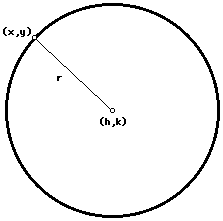
by definition, a point (x,y) is on this circle if and only if the distance from (x,y) to (h,k) is r. Thus we have or .
The center is the point (h,k) and the circle has radius r.
So, how is a circle formed from a plane intersecting a right circular cone.
The plane has to be parallel to the xy-plane, and for it to be a circle z is not equal to 0. In this case, the intersection is a point.
So if the above equation is expanded, you get in which h, k, and r are constants. Therefore, the general form for the equation of a circle is

When the equation of a circle is given in general form, it can be rewritten to find its center and radius by completing the square.

Now I will start with the basic equation for a circle like . This is the unit circle, and has many applications is trigonometry. When graphed it looks like the following.

So, what do different values for D, E, and F do to the graph of the circle.
If E = 1, and F = 0 and we let D = -3, -2, -1, 1, 2, 3, you get the following picture

It appears that the circle grows, but maintains the x-intercept values. 2 of the above equations are as follows

So, if we set x = 0 in both of these we get

And, therefore, our x-intercepts are the same.
If we complete the square on the above 2 equations we get the following equations

The centers are at (-1/2, -1/2) and (1/2,-1/2) and radius (sqrt(2))/2.

We can go through a similar process to see what effect changes to the E and F values have on the graph.
For a more geometric approach to circles, Click Here to view a 10-day unit on the geometry of circles.

Parabolas

The graph of any quadratic function is a parabola. Quadratic functions are of the form

where a, b, and c are constrants and a is not zero. So all parabola's are similar in shape to the graph of (As seen in the following picture).

Here, the vertex is the point (0,0) and the axis of symetry is the y-axis.

By completing the square, the equation of the parabola

can be rewritten as

where the vertex of the parabola is (h,k) and the axis of symetry is the line x=h. Let's look at a few graphs and do some algebra and see what we can figure out about different values for a, b, and c using Algebra Expressor.

In the following picture I let b = 0, c = 0, while setting a = -3, -1, -1/2, 1/2, 1, and 3.

Therefore, you can see the parabola opens upward if a > 0 and downward if a < 0.
There also appears to be another pattern. It looks like if the absolut value of a is greater than 1 then the the curve is wider and if it is smaller it is more narrow. Does this match what we know about parabolas?

In the next picture I let a = 1, c = 0, while setting b = 1

The equation of the above graph is

and if we complete the square, we get the equation

Therefore, our vertex is ( -1/2, -1/4) and the line of symetry is x = -1/2. Is this reinforced by the graph? So, what is b doing to the graph. It looks like setting b = 1 moved the graph of in the negative x direction by 1/2 and the negative y direction by 1/4. What does other values for b do?
In the following picture a = 1, c = 0, and b = -3, -1, -1/2, 1/2, 1, and 3.

Therefore this is the picture of the graph of the following equations:

How is each equation moving the graph of the original equation in the form . What if we were to complete the square for these equations? And, what if we had a different value for a?
In the following picture a = -1, c = 0, and b = -3, -1, -1/2, 1/2, 1, and 3.

Now, compare this with the previous graph. This is fairly reinforcing.
If we just look at the equation in which a = -1, b = -3 and c = 0, and we get the following picture

If we complete the square of , we get the equation .
So, what changes have the values of a and b made to the graph . The negative appears to have inverted the graph. The gragh also appears to be moved over to the left 3/2 and up 9/4. Where do these two graphs intersect? If we set them equal to each other, they intersect at the points (0,0) and (-3/2, 9/4).

Maybe one more will help us make some decions about what is going on.

In the following picture a = 3, c = 0, and b = -3, -1, -1/2, 1/2, 1, and 3.

If we just look at the equation in which a = 3, b = -1, and c = 0, and we get the following picture.

If we complete the square of , we get the equation .
So, what changes have the values of a and b made to the graph .The graph appears to be moved over to the right 1/6 and down 1/12. What is different about where these two graphs intersect?
The 3 is what is making the graph of more narrow than that of .

Now let's look at different values for all a, b, and c for .
If we set a = 1, b = 1 and let c = -3, -1, -1/2, 0, 1/2, 1, 3 , we get the following picture.

It is fairly easy to see what is going on with the c values.
There are also parabolas of the form

Such a parabola is expressed in the following picture

The equation of this parabola is . Similar investigations can be done with a parabola whose directrix is parallel to the y-axis. The investigations above involved parabolas whose directrix is parallel to the x-axis

How can we use a spreadsheet to investigate parabolas. The following is a graph created in Excel

Using the following columns



In which the B-column contains the formula: A1*A1-10*A1+25

A more geometric definition of the parabola is the set of all points in the plane equally distant from a fixed line and a fixed point not on the line. The fixed line is called the directrix. The fixed point is called the focus. The following is part of a parabola created using GSP.

I started with line AB and a point C on that line. I constructed a perpendicular line k to line AB through C. Then I pick an arbitrary point not on the line which will be the focus, point D. Find the midpoint on the segment CD and construct the perpendicular through this point, F. Where this line intersects k is the point, G, of tangency, and the perpendicular, m, through F is the line tangent to the parabola. Click here to view the animation in GSP. As C moves along AB G traces the parabola.

The Ellipse

The standard form of the equation of the ellipse with center at (h,k) and major axis of length 2a units, where , is as follows:
, when the major axis is parallel to the x-axis
or
, when the major axis is parallel to the y-axis

An example of an ellipse graphed using algebra expressor is as follows

The equation of this ellipse is .
Another example is as follows


A more geometric definition of the ellipse is the set of all points in the plane, the sum of whose distances from two fixed points is constant. Each fixed point is called a focus. The following is an ellipse created using GSP.

The construcstion is as follows:
Construct any point C on the circle. Construct a segment through point C and the center of the circle, A. Construct another point D within the circle. Construct segment CD. Find the midpoint, F, of this segment. Construct the line perpendicular to CD, through F. Find the point of intersection of this line with the line through CA. Trace that point, H, as the point C travels along the circumference of the circle.
The following is the picture with the appropriate labels.

D and A are the foci, and V1-V4 are the vertices. H is the point that defines the ellipse.
Click here to view the GSP file that demonstrates this. As D is moved within the circle, you will get a different ellipse as seen in the following picture.


The Hyberbola

The standard form of the equation of a hyperbola with center at (h,k) and tansverse axis of lenght 2a units, where , is as follows.
, when the transverse axis is parallel to the x-axis,
or
, when the tansverse axis is parallel to the y-axis.

An example of a hyberbola graphed using Algebra Expressor is as follows:

The equation of this hyberbola is

The equation of this hyberbola is .


A more geometric definition of a hyperbola is the set of all points in the plane, the difference of whose distances from two fixed points is a positive constant. How can we use the GSP construction above to create a hyperbola.

The above hyberbola was constructed by moving the point in the ellipse construction above outside the circle. The following is the picture with the appropriate labels.

As D is moved around on the outside of the circle, you will get a different hyberbola. Click here to view the GSP file that demonstrates this. The following is an example of such a hyberbola.

And that concludes my investigation of conics. Of course, you can see that there are several different ways you can explore conics using different computer software.