Constructing Polygons from Triangles

by
Jennifer Roth

Given the line segment AB, construct an isosceles triangle

Construct a circle of radius AB from a point on a line, and a a circle from another point C on the same line with radius AB (AC has to be greater than or equal to 2AB). Where these two circles intersect, is your third point for your isosceles triangle (there are two such points).

Click here to view the GSP file that demonstrates this.

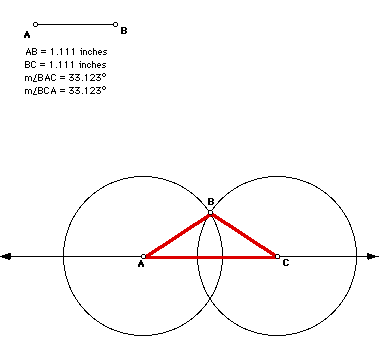
Now, how can we construct a parallelogram using this isosceles triangle.
If you reflect triangle ABC in AC you get the following parallelogram

Click here to view the GSP file that demonstrates this. This parallelogram has sides of equal length.

It is a special kind of parallelogram, a rhombus, in which all four sides are congruent and its diagonals are perpendicular.
Therefore, you would get a square if you started with a 45-45-90 triangle.

How could we produce a rectangle using a any right triangle. A simple construction using perpendicular lines will produce the following if you start with triangle ABC. (How else can we do this using reflections and translations?)

Now, how could we use any right triangle to produce a parrallelogram.

Click here to view the script that demonstrates this. If you first reflect the triangle ABC in AC you get triangle ACD. Then, if you reflect triangle BCD in DB you get the parallelogram BCDE. This parallelogram, again, has equal sides. (How else can we do this?)

How can we construct a parallelogram using any triangle. Would this give us a parallelogram that has different side lengths. Construct triangle ABC and construct a line parallel to AC through B. Use this as your line of reflection for triangle ABC. Then construct segment AA' and segment CC'. You get a special parallelogram, another rectangle.

Click here to view the GSP file that demonstrates this. How else can we use any triangle to produce a parallelogram?

Now, how do we construct any quadrilateral using triangles. Reflect along one of the sides of the triangle, except for a right triangle, and you will get a quadrilateral.

How do we construct a trapezoid using triangles.

Construct triangle ABC, and construct any point on AC. Then, construct a line parallel to BC through this point, D. If you started with an isosceles triangle, you would get an isosceles trapezoid. As the line segment ED approaches length 0, the limit is your original triangle.

So, how can we construct other polygons using triangles. I will just focus on regular figures (figures that are equilateral and equiangular).

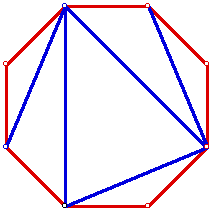
As we know the measure of each interior angle of a regular n-gon is 1/n(n-2)(180 degrees). Therefore the pentagon above was constructed by rotating a line segment 108 degrees, and the hexagon was constructed rotating a line segment 120 degrees, etc. As you can see the (n-2) is the number of triangles used to make up each of the polygons.
Click here to view the GSP script used to construct the Pentagon.
Click here to view the GSP script used to construct the Hexagon.
Click here to view the GSP script used to construct the Octagon.

What if we were to use an isosceles triangle with the base angle equal to 1/n(n-2)(180 degrees) and the other vertices at the center of the regular n-gon? We could rotate this triangle the 1/n(n-2)(180 degrees) about the center to produce the n-gon.