for different values of a, b, or c as the other two are held constant.
From these graphs discussion of the patterns for the roots of
can be followed. For example, if we set
for b = -3, -2, -1, 0, 1, 2, 3, and overlay the graphs, the following
picture is obtained.
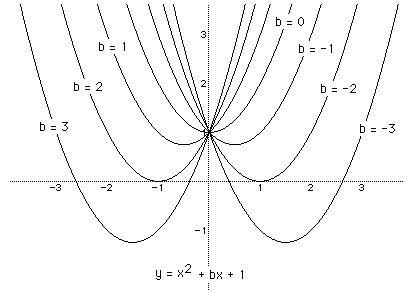
We can discuss the "movement" of a parabola as b is changed.
The parabola always passes through the same point on the y-axis ( the point
(0,1) with this equation). For b < -2 the parabola will intersect the
x-axis in two points with positive x values (i.e. the original equation
will have two real roots, both positive). For b = -2, the parabola is tangent
to the x-axis and so the original equation has one real and positive root
at the point of tangency. For -1 < b < 2, the parabola does not intersect
the x-axis -- the original equation has no real roots. Similarly for b =
2 the parabola is tangent to the x-axis (one real negative root) and for
b > 2, the parabola intersets the x-axis twice to show two negative real
roots for each b.
Now consider the locus of the vertices of the set of parabolas graphed from
Show that the locus is the parabola
Generalize.
If we combine the locus with the original graph, we get the following graph:
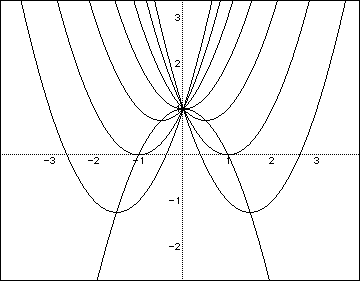
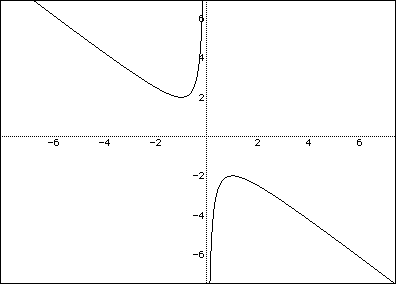
Consider again the equation
Now graph this relation in the xb plane. We get the following graph.
If we take any particular value of b, say b = 3, and overlay this equation
on the graph we add a line parallel to the x-axis. If it intersects the
curve in the xb plane the intersection points correspond to the roots of
the original equation for that value of b. We have the following graph.
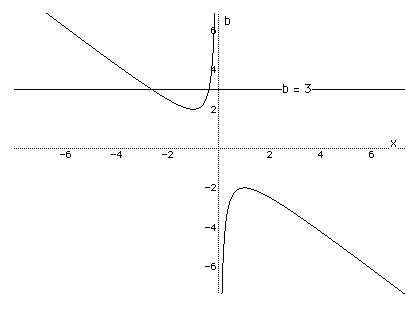
For each value of b we select, we get a horizontal line. It is clear
on a single graph that we get two negative real roots of the original equation
when b > 2, one negative real root when b = 2, no real roots for -2 <
b < 2, One positive real root when b = -2, and two positive real roots
when b < -2.
is considered. For example, if we set the equation
for c = -4, -2, , 0, 2, 4, 6, 7 and overlay the graphs, the following
picture is obtained.
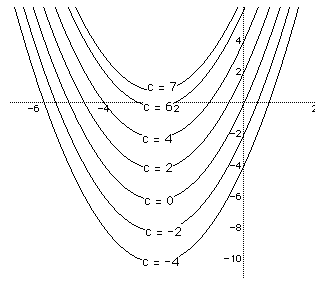
Where is the locas of the vertices of the parabolas?
Show that the locus is the line:
How is this line found?
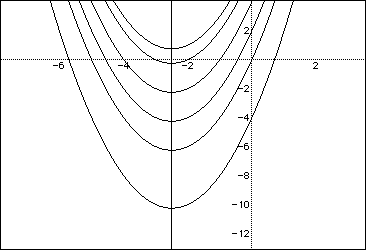
If we add this line to the original graph of varying values for c, we get
the following graph:
If the equation is graphed in the xc plane, it is easy to see that the
curve will be a parabola. For each value of c considered, its graph will
be a line crossing the parabola in 0, 1, or 2 points -- the intersections
being at the roots of the orignal equation at that value of c. In the graph,
the graph of c = 1 is shown.
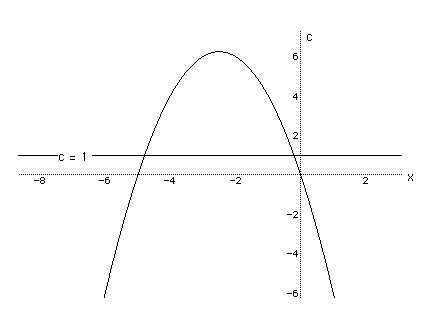
It is easy to see that when c = 1, the equation
has two negative roots.
There is one value of c where the equation will have only 1 real root --
at c = 6.25. For c > 6.25 the equation will have no real roots and for
c < 6.25 the equation will have two roots, both negative for 0 < c
< 6.25, one negative and one 0 when c = 0 and one negative and one positive
when c < 0.
How are these values found?
In the following example the equation
is considered.
For example, if we set a = -3, -1, -1/2,0, 1/2, 1, 3 and overlay the graphs,
the following picture is obtained.
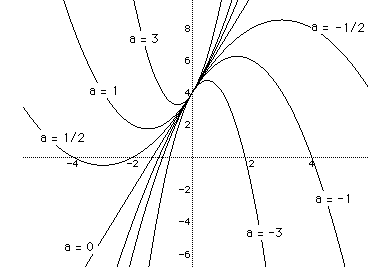
If we graph the equation in the xa plane we get the following picture:
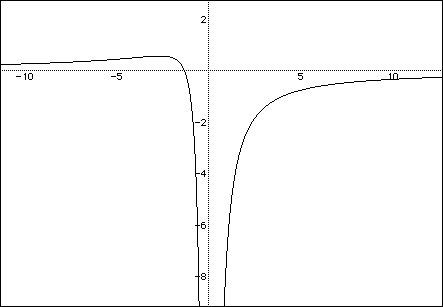
In the following graph , the graph of a = 0 is shown.
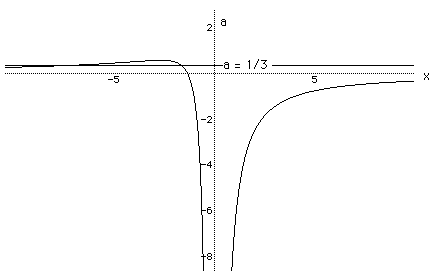
From the graph it appears that you will get 0, 1, or 2 roots for the
equation
For which values will there be no roots, 1 root, or 2 roots?
Further investigation could include similar investigations as above for
different values for a, b, and c. What pattern can you see develop, if any?