Investigation of the
Construction of Equilateral Triangles
on Each side of any Given Triangle

by
Jennifer Roth

Given any Triangle we can construct equilateral triangles externally on each side. This is accomplished by rotating each side of the triangle out 60 degress. The following was produced by completing this procedure using Geometer's SketchPad (GSP).

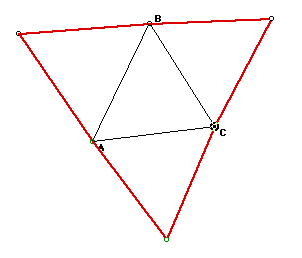
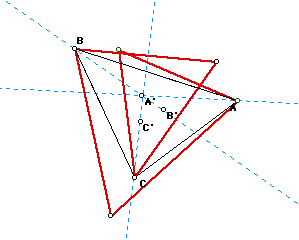
The three red triangles are thus all constructed to be equilateral. Now we will locate the centroid of each triangle and label them A', B', and C' (Where A' is opposite A, B' is opposite B, and C' is opposite C). And then we constuct lines AA', BB', CC'.

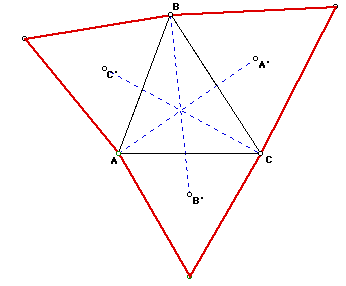
As points A, B, and C are translated, the lines AA', BB', and CC' remain concurrent. Click here to view the GSP file that demonstrates this.

This point of concurrency, say P, is not the orhocenter, centroid, incenter, or circumcenter of "any" triangle ABC. If we find these four points for ABC we can demonstrate that none of these points is the same as point P. But, there are also many other things going on in this construction.

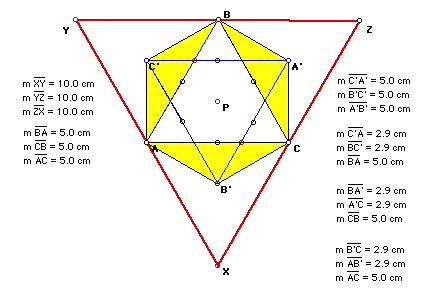
The simplest case is when the given triangle ABC is an equilateral triangle (As shown above). In this case the orthocenter, centoid, incenter, and circumcenter are all equal to P (And this is only true for this case). If we construct these four points they will all overlay P. The larger triangle created XYZ is also an equilateral triangle.
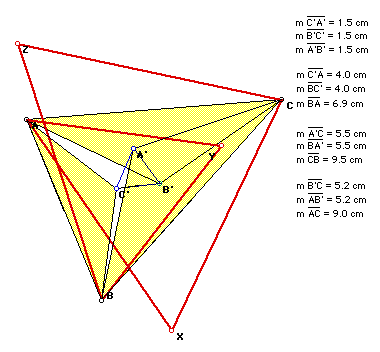
The Triangles ABC', ACB', and CBA' are all iscoceles, and the triangle A'B'C' is equilateral. These two things are also true, however when ABC is not equilateral. (See the following picture)

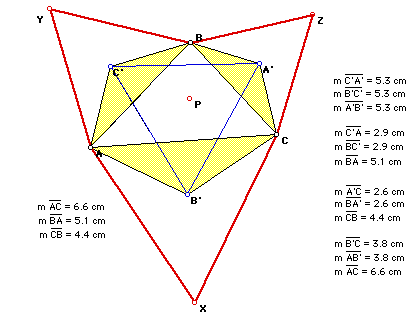
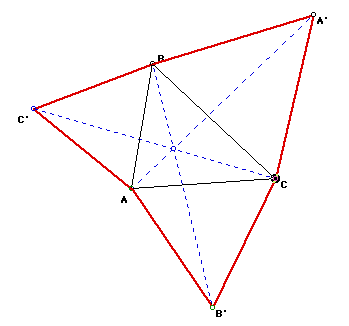
If we were to translate A, B, and C, then ABC', BCA', and ACB' remain iscoceles, and A'B'C' remains equilateral. Click here to view the GSP file that shows this animation.

We can also do a similar construction using a square.

Similar Construction with the Constructed triangles
Overlapping the Given Triangle

As in the above construction, if we overlap the triangles, then it appears the lines AA', BB', and CC' remain concurrent.

It also appears that our other conclusion hold true for this construction also.

Similar Construction with A', B', and C' defined as the external
vertices of the externally constructed equilateral triangles.


If the points A, B, and C are translated, the lines AA', BB', and CC' remain concurrent. Click here to view the GSP file that demonstrates this. Through further investigation, more things can be found out about this construction. It can be shown that AA' = BB' = CC'. Click here to view the GSP file that demonstrates this. As the points are translated, the lengths remain equal.

Constuction of a Square on Each Side
of Any Given Triangle

We can construct a square on each side of any given triange by rotating the sides of the triangle out 90 degrees. And let A', B', and C' be the centers of the squares.

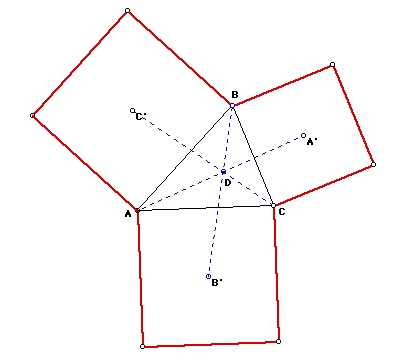
The point D is the point of concurrency for the three lines AA', BB', and CC'. Click here to view the GSP file that demonstrates this.

The triangle AC'B, CA'B, and AB'C are all isosceles triangles.

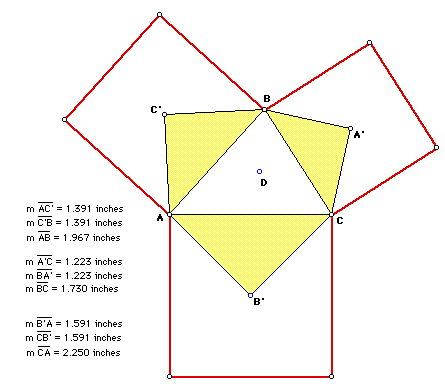
But unlike the constuction with the equilateral triangles, when we construct the squares, the Triangle A'B'C' is not equilateral. Click here to view the GSP file that demonstrates this.

If the given triangle is a right triangle, then we will get a representation of the Pythagorean Theorem as follows.


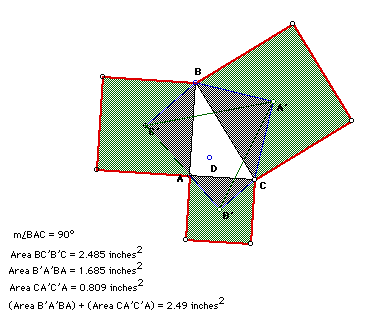
Further investigations might include other regular figures constructed on the sides of a triangle, or using other regular figures as the base. For example, what if the center figure is a square and you draw triangles on the sides.

Back to Jennifer's Home Page