The following is an exploration of triangles using Geometer's SketchPad
(GSP). We are attempting to construct various triangles, then construct
other geometric constructions on their given sides. This exploration would
be extremely difficult without the advantge of having GSP as a tool.

The GSP file for this construction can be recalled by clicking here
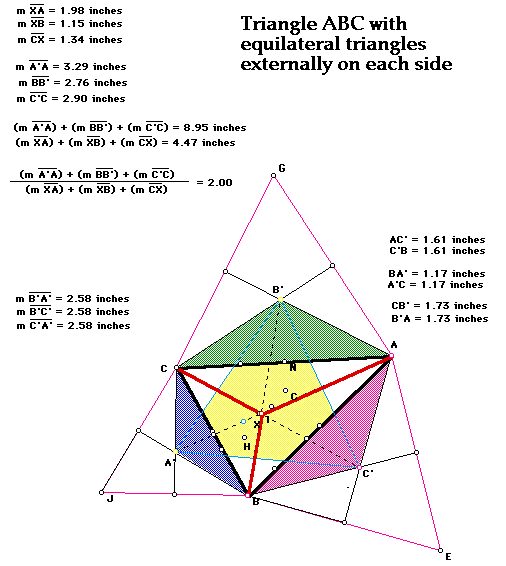
The original triangle is ABC. An equilateral triangle has been drawn corresponding
to each side A, B, and C. In each of these equilateral triangles, the centroid
was found and labeled. A' is the centroid of triangle BCJ. It is opposite
the A vertex. Each centroid has been connected to its opposite vertex in
the original triangle ABC. The point of concurrency inside triangle ABC
is X. After drawing the orthocenter (H), circumcenter (c), centroid (G),
and incenter (I) of original triangle ABC, it is found that none of these
points are the same as X. Point X is its own unique point and does not correspond
to any of the other four. Connecting A', B', and C', constructs a fourth
equilateral triangle (yellow shaded area). Connecting each centroid to its
two adjacent vertexes gives three distinct isosceles triangles. Triangle
A'BC (purple area), triangle C'BA (light blue area), and triangle B'AC (green
area). Also, a relationship was found when summing the lengths of the three
centroids to the opposite vertexes (i.e., AA', BB', CC') and summing the
lengths of the three vertexes to point X (i.e., XA + XB + XC). This ratio
of the sums is always 2.00. To test any of these ideas hit above and feel
free to move the vertexes of triangle ABC as you please. If either angle
ABC, angle ACB, or angle CAB are greater than 150 degrees, the point X lies
outside of the original triangle ABC This occurs when the centroids lie
on a line with two points of original triangle ABC. For example, when A',
B, and A are on a line ( with B between A and A') the point X lies on this
line as well and the angle is 150 degrees. If original triangle ABC is constrcuted
as an equilateral trianlge, then point X X and the four centers of the triangle
ALL occur at the same place. This can be best illustrated by clicking
above and rotating points A, B, or C. Observe the angle measurements and
point X.
The GSP file for this construction can be recalled by clicking here.
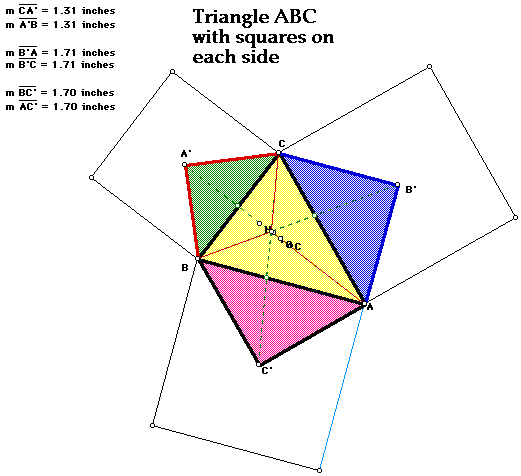
This second construction is a construction of a triangle ABC with squares
constructed on each side of the triangle. The sides of the squares are equal
to the corresponding sides of the original triangle. A', B' and C' are the
centers of the three squares, respectively. Constructing segments from A'
to A, B' to B, and C' to C (red dashed lines) gives us a point of concurrency
inside triangle ABC. Again, this point is not the same point as the orthocenter,
cetroid, circumcenter, or incenter of the original triangle ABC. Connecting
the three points A', B' and C' to form a triangle does not form an equilateral
triangle, or one of any significance to this construction. Three distinct
isosceles triangles are formed from construction of a center of one of the
squaresand the two adjacent points of the original triangle ABC. Triangle
ABC', triangle BCA', and triangle ACB' are all isosceles with base equal
to a side of the original triangle ABC. Click above to play with and explore
this construction.
The GSP file for this construction can be recalled by clicking here
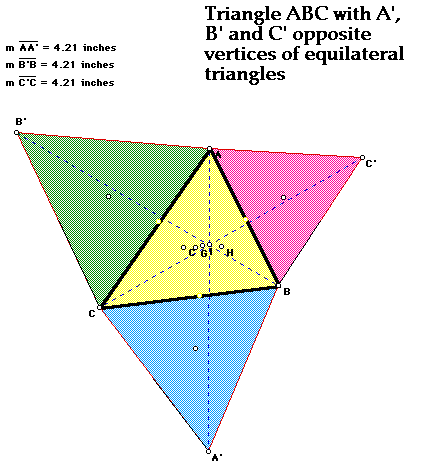
Constructing triangle ABC with equilateral triangles on each side (same
as first construction) gives a construction as the one above. Labeling A',
B', and C' as opposite vertices of the original triangles and drawing segments
from A' to A, B' to B, and C' to C gives three dashed lines with a point
of concurrency inside original triangle ABC. The three segments are of equal
length. Again, the point of concurrency is different from the orthocenter,
incenter, centroid, and circumcenter of original triangle ABC. The point
of concurrency is inside triangle ABC when angle B'CB creates a positive
angle with respect to BC. This is true for all three angles. In this triangle,
when angle ABC, angle BAC, or angle ACB are greater than 120 degrees, the
point X is outside the original triangle ABC. This occurs becuase an equilateral
triangle has three congruent interior angles of 60 degrees, and therefore
all supplementary angles will equal 120 degrees. of This can be better understood
by clicking above and rotating points A, B, and C and observing the angle
values and point X.
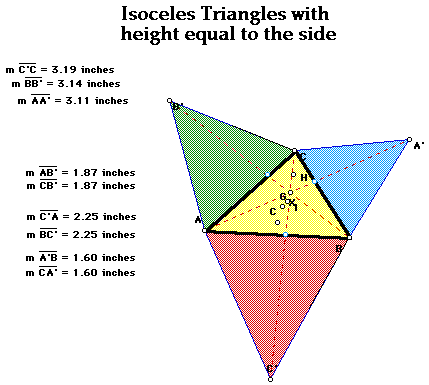
The GSP file for this construction can be recalled by clicking here
Constructing three isosceles triangles with height equal to the corresponding
side of triangle ABC (yellow area) gives us the above representation. Labeling
the opposite vertices A', B', and C' and drawing segments from A to A',
B to B', and C to C' gives us the following picture. Point X is the point
of concurrency for the three segments. Once again, point X is unique from
the orthocenter, incenter, circumcenter, and centroid of triangle ABC. Three
isosceles triangles have already been constructed (blue, green and orange
shaded areas) and no other significant triangles were found.
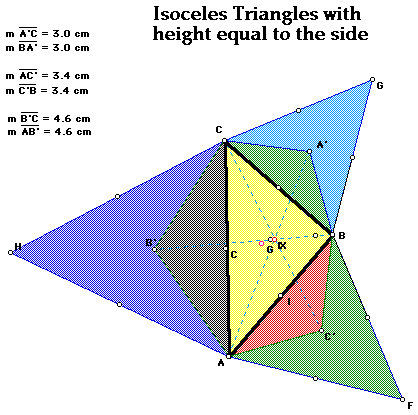
The GSP file for this construction can be recalled by clicking here
This construction is the same as above, but the centroids of the three isosceles
triangles have been constructed and designated A', B', and C', respectively.
Segments have been constructed from A' to A, B' to B, and C' to C. Point
X is the intersection of the three segments. Three unique isosceles triangles
are formed from points A', B', and C' to their adjacent vertexes. Triangle
A'BC, triangle B'AC, and triangle C'AB are all isosceles with a base equal
to a side of the original triangle.
The GSP file for this construction can be recalled by clicking here
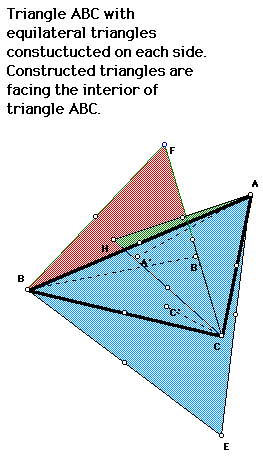
This construction is a difficult one to view here and is much easier to
understand by clicking above, but we will try to explain nonetheless. ABC
is the original triangle and three equilateral triangles have been constructed
facing the interior of each side. A', B', and C' are the centroids of the
three constructed equilateral triangles. Constructing segments from A' to
A, B' to B, and C' to C gives us three segments that do not neccessarily
intersect at a common point. Selecting point A, B, or C and moving around,
sometimes the points intersect. If the three points are made into an equilateral
triangle, then all 4 triangles overlap with A', B' and C' being concurrent
at the centroid, orthocenter, incenter and circumcenter of triangle ABC.
In conclusion, constructions of various triangles and squares on the sides
of an original triangle is an exercise that is highly useful to illustrate
properties of triangles. Concepts such as the 4 centers of a triangle, isosceles
triangles, equilateral triangles, altitude, and points of concurrency are
all developed and discussed. Explorartions with the GSP allow students to
visualize the arguments made, that otherwise would be very difficult to
do. Without GSP, one would have to construct hundreds of triangles to reach
solutions, but with GSP a student can move points as they please and attempt
to draw conclusions based on their explorations.