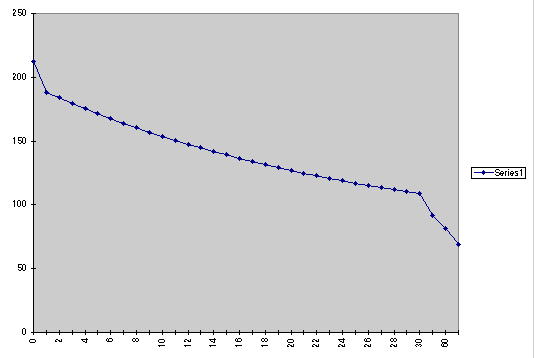
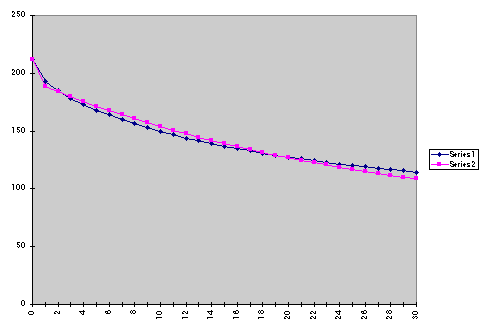
Graph of time (x-axis) vs. temperatures observed (y-axis)
This is to be an exploration of boiling water temperatures. The process
was to to bring 2 cups of water to a boil and then transfer the water to
a separate cup for cooling. The initial temperature of the boiling water
was recorded as 212 degrees fahrenheit and then temperatures of the cooling
water were recorded every minute for 30 consecutive minutes. The following
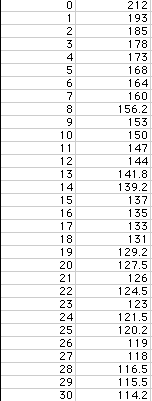
is a chart for time (column 1) and temperatures observed (column 2). Following
that is the graph of the same data.


The next step was to attempt to construct a formula to fit our plotted
data. Dr. Wilson had previously explained to the class that an exponential
equation would be used for this problem, and using Microsoft Excel, the
process was rather easy. Generating a function with Excel saves time and
effort. We first thought that our equation was in the form of y= a * e^x
+ c. We needed our intial value to equal 212 and after 300 minutes, we hypothesized
that the temperature would be approximately equal to the room temperature
of 69 degrees. The formula we tried was (212-69)*(e^-.06*temp) + 69. The
-.6 was a random choice. To check the validity of our equation, we took
the square of the difference for each time, summed the squares and divided
by 31 ( data points). This statistic turned out to be over 250 for the given
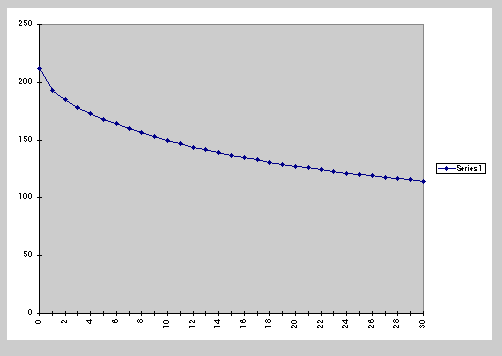
equation. Now, our job was to play with the values until a graph similar
to ours was generated and the statistical value was as close to 0 as possible.
After many attempts, the statistic could not be brought down lower than
about 120. We had difficulty with the initial few values because the drop
in the first minute was so great, 19 degrees. After the first minute, the
numbers dropped more consistently. So, we decided to omit the first minute
in our equation and begin with 193 degrees in our equation. The equation
that dropped the statistic to the lowest value was (193-69)*e^(-.038 * temp)
+ 69. The statistic equaled 10.23. The following is a table of the time
(column 1), temperature recorded (column 2), the equation values (column
3), the difference between the equation values and the actual temperature
recorded (column 4) and the squares of the difference (column 5). Then,
a graph of the table is presented.
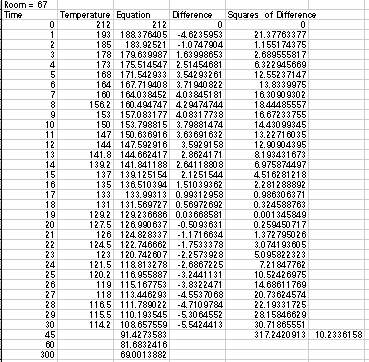
The next graph is a graph of the time vs. the predicted values. The three
extra plotted points are the predicted temperatures for 45 minutes, 60 minutes,
and 300 minutes after the water was transferred from the pan to the cooling
cup. After 45 minutes, the equation predicts that the temperature will be
91.4 degrees, and after 60 minutes the temperature will equal 81.7 degrees
fahrenheit. The equation was constructed so that the final value would equal
the room temperature at the begining of the lab and as seen, it does. The
temperature after 300 minutes is 69 degrees fahrenheit.