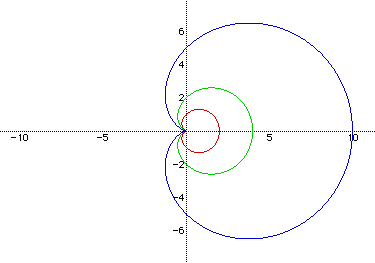

Three graphs have been constructed above. The red cardioid has the equation
r=1+cos(t). The green cardioid has the equation r=2+2cos(t). The blue cardioid
has the equation r=5+5cos(t). Notice that the graph is symmetric with the
x axis.
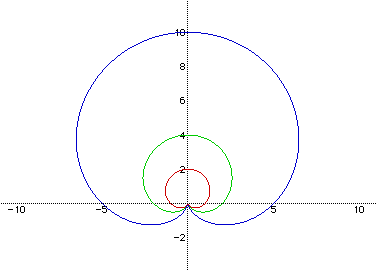
Now, keeping the value of k equal to 1, let's see what happens when a<b:
Red Cardioid: r=cos(t)
Green Cardioid: r=1/2 +2cos(t)
Blue Cardioid: r=3+6cos(t)
Brown Cardioid: r=6+7cos(t)
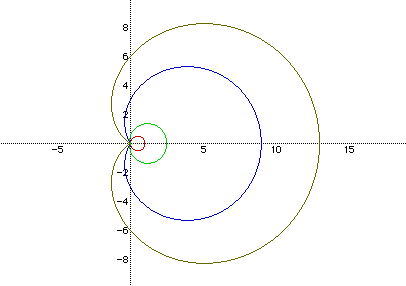
Again, holding k=1, let's see the graphs when a>b:
Blue Cardioid: r=8+7cos(t)
Green Cardioid: r=5+1/2(cos(t))
Brown Cardioid: r=10+2cos(t)
Red Cardioid: r=3+2cos(t)
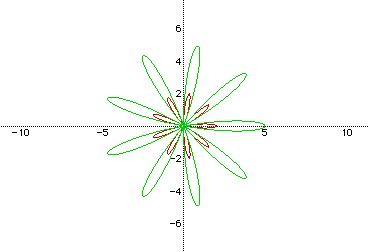
Here, the green "rose" has the equation r=5cos(9t). Notice that there are 9 "leaves" of the green rose and that when b=5, the graph is located between values of x=-5 and x=5. The red rose has the equation r=2cos(9t). Again, there are k=9 leaves of the rose, but this time, the graph lies between x=-2 and x=2.
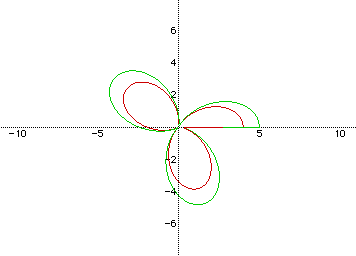
Red Cardioid: r=2+2cos(5t/2)
Green Cardioid: r=5/2 + 5/2 cos(5t/2)
The red cardioid spans from x=-2 to x=2. Since the red and green
cardioids have a k value of 5/2, there are exactly 2.5 leaves on each rose,
and the green rose spans from x,y =-2.5 to 2.5.
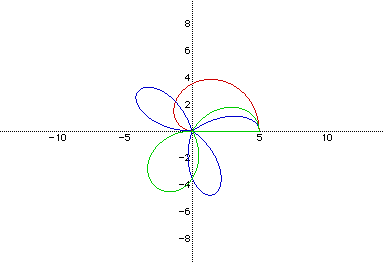
Red Rose: r=5cos(t/2)
Green Rose: r=5cos(3t/2)
Blue Rose: r=5cos(5t/2)
Here, we see again that the value of k alters the number of leaves on
the rose. The red rose has one-half a leaf; the green rose has one and one-half
leaves; and the blue rose has two and one-half leaves.
The b value of 5 stretches the roses to x and y values of -5,5.
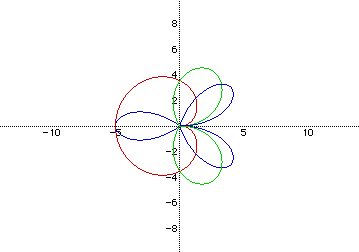
Red Rose: r=5sin(t/2)
Green Rose: r=5sin(3t/2)
Blue Rose: r=5sin(5t/2)
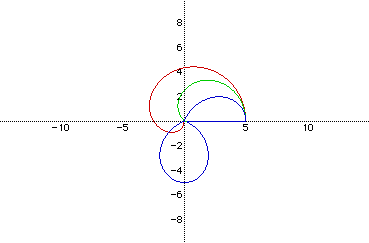
Green Rose: r=5cos(t/3)
Red Rose: r=5cos(2t/3)
Blue Rose: r=5cos(4t/3)
Again we see that the k value alters the number of leaves on the rose, while
the b value determines the span of the curves along the x and y axes.
Keeping the same values for a, b, and k, let's view the sine graph:
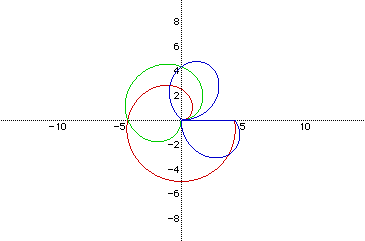
Red Rose: r=5sin(t/3)
Green Rose: r=5sin(2t/3)
Blue Rose: r=5sin(4t/3)
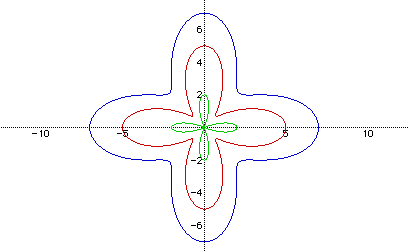
Green rose: r=2cos(4t)
Red rose: r=3+2cos(4t)
Blue rose: r=5+2cos(4t)
Whereas the green rose spanned to x and y values of -2 and 2, the red rose spans from x,y =-5 to 5 and the blue rose spans from x,y=-7 to 7. Notice that the value of a stretches the graph a units from the original equation.
Keeping the same values of a, b, and k for the sine graph shifts the green, red, and blue roses so that they are no longer symmetric to the y axis, but only symmetric to the origin: