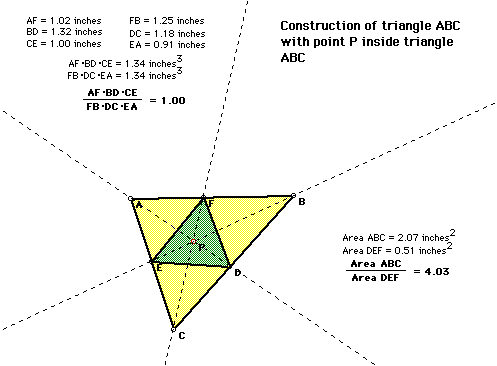
This exploration is accomplished using Geometer's Sketchpad. To begin
I constructed a triangle ABC (yellow shaded area) and a random point P inside
the triangle ABC. Next, I constructed 3 unique lines, one from each vertex
through point P. Points D, E , and F are the points where the lines intersected
triangle ABC. Points DEF were connected to form a triangle (green shaded
area).
Exploring segments AF, BD, and CE, compared to segments FB, DC, and EA,
I could made interesting hypotheses. The ratio was found to equal precisely
1.00. No matter where point P was located inside triangle ABC this ratio
of (AF)(BD)(CE)/(FB)(DC)(EA) equaled 1.00.
Also, I compared the area of triangle ABC to the area of triangle DEF. The
ratio of ABC/DEF never got below 4.00.

To explore the above construction, click here
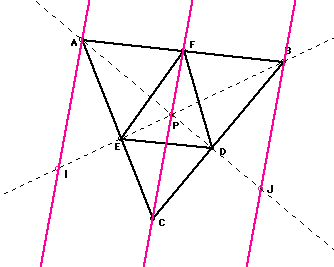
PROOF:
Triangle PBF is similar to triangle IBA and triangle PAF is similar to triangle
JAB, because corresponding angles are congruent. Now, we get
and since triangle AEI is similar to triangle CEP and triangle BDJ is
similar to CDP ( alternate interior angles and vertical angles are congruent),
we can say that
From the similar triangles we can get the following ratios:
![]() ,
, ![]()
Working with the second two ratios I got,
Then, using the first two ratios, along with this new one, I got
Then simplifying the right side of the equation gives me
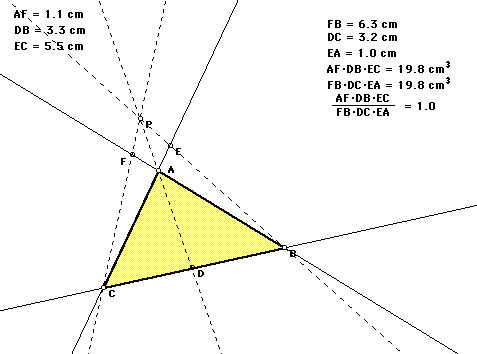
To find out when the ratio of the area of triangle ABC to the area of
triangle DEF equals 4.00, I hypothesized that this would occur when all
four triangles inside triangle ABC were equal, regarding their area. So,
triangle DEF, triangle AEF. triangle BFD, and triangle CED must all have
equal areas. The most logical way this would occur would to have equal sides
involved and I could make the sides equal by constructing the midpoints
of segments AB, BC, and AC, then constructing the three medians of triangle
ABC. As shown below, this gives me four equal triangles inside triangle
ABC, thus the ratio of triangle ABC to triangle DEF = 4.00. To see this
construction on GSP, click here
Back to Brian Seitz's homepage