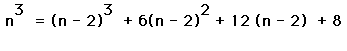Painted Sides of a Cube

by Brian Seitz and Inchul Jung

Problem: Given a 2 x 2 x 2 cube made of 8 1 x 1 x 1 blocks. If the cube is painted, then each of the blocks has 3 of its faces painted.

If a 3 x 3 x 3 cube is painted, a given block may have 0, 1, 2 , or 3 of its faces painted.

Count how many of each.

Do the same for a 4 x 4 x 4 cube, a 5 x 5 x 5 cube, and a n x n x n cube.

Here is a 3 x 3 x 3 cube:

These 3 cubes all represent 3 x 3 x 3 cubes, the first one has the blocks shaded (pink) that will be painted 3 sides, the second cube has the blocks shaded (blue) that will have 2 sides painted, and the third cube has blocks shaded (green) that will have 1 side painted.

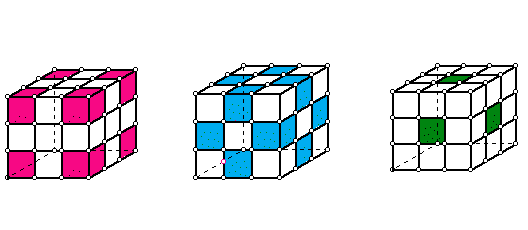
Now, let us see an example of a 4 x 4 x 4 cube, then below is three 4 x 4 x 4 cubes with the cubes that will be painted 1, 2, and 3 sides.

 

 

 

There is a definite pattern for the cube and the sides painted.
After looking at the first 4 cubes, the sides painted look as such:

 

In a 2 x 2 x 2 cube there are:
0 blocks with 0 sides painted.
0 blocks with 1 side painted.
0 blocks with 2 sides painted.
8 blocks with 3 sides painted.

In a 3 x 3 x 3 cube there are:
1 blocks with 0 sides painted.
6 blocks with 1 side painted.
12 blocks with 2 sides painted.
8 blocks with 3 sides painted.

In a 4 x 4 x 4 cube there are:
8 blocks with 0 sides painted.
24 blocks with 1 side painted.
24 blocks with 2 sides painted.
8 blocks with 3 sides painted.

In a 5 x 5 x 5 cube there are:
27 blocks with 0 sides painted.
54 blocks with 1 side painted.
36 blocks with 2 sides painted.
8 blocks with 3 sides painted.

 

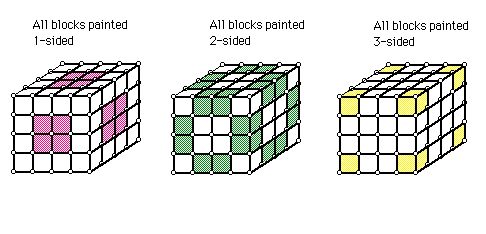
We attempted to look for a pattern after constructing the first few cubes and looking at the trends in sides painted for each cube.

For 0 sides painted, we found that if n = (the number blocks on one row or column of the cube), then (n-2)^3 is the number of cubes with 0 sides painted.

For 1 side painted, we found that the pattern was 6(n - 2)^2 = the number of cubes with 1 side painted.

For a cube with 2 sides painted, we found that the pattern was 12(n - 2) = the number of cubes with 2 sides painted.

For the cubes with 3 sides painted, it will always be 8. The eight painted cubes are the 8 corners of any and all cubes.

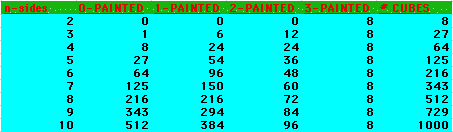
The spreadsheet below takes you through the first nine cunes with n x n x n sides.

 

Now, we have found these four values for our cubes with n sides:

looking at the four values, one notices that the values are the products of a binomial expansion.

 

the expansion of the binomial looks as such

 

Brian Seitz's homepage