Some different Ways to Examine
by
James W. Wilson and Michael R. Akes
University of Georgia
It has now become a rather standard exercise in Algebra II, with available
technology, to construct graphs to consider the equation
and to overlay several graphs of
for different values of a, b, or c as the other two are held constant.
From these graphs discussion of the patterns for the roots of
can be followed. For example, if we set
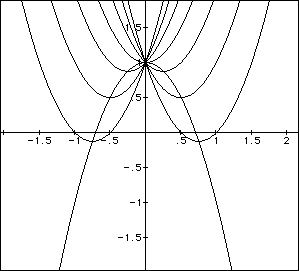
for b=-3, -2, -1, 0, 1, 2, 3, and overlay the graphs, the following picture
is obtained
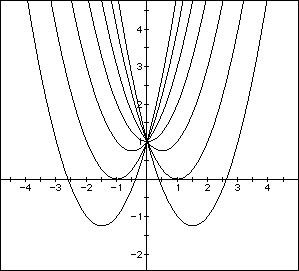
We can discuss the "movement" of a parabola s b is changed.
The parabola always passes through the same point on the y-axis (the point
(0,1) with this equation). For b < -2, the parabola will intersect the
x-axis in two point with positive x values (ie. the original equation will
have two real roots, both positive). For b=-2, the parabola is tangent to
the x-axis and so the original equation has one real and positive root at
the point of tangency. For -1 < b < 2, the parabola does not intersect
the x- axis - - the original equation has no real roots. Similarly for b=2
the parabola is tangent to the x- axis (one real negative root) and for
b > 2, the parabola intersects the x- axis twice to show two negative
real roots for each b.
Now consider the locus of the vertices of the vertices of the set of parabolas
created from
We can show that the locus is the parabola
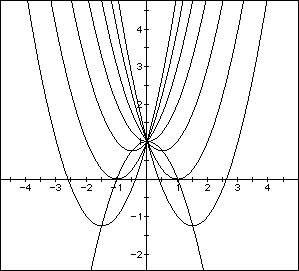
The locus of the vertices is being controlled by the c term at
the end and the fact that they all have the same a term. Notice what
happens if we change the c=1 to c=2.
Now we have changed the locus of the vertices to
The following picture shows this
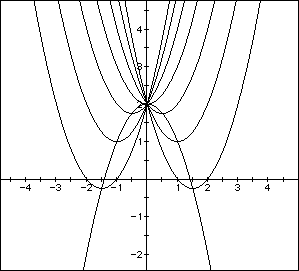
We should now consider the a term. Notice what happens if we can the
a=1 to a=2 and we leave the a coefficient the same on the locus's graph
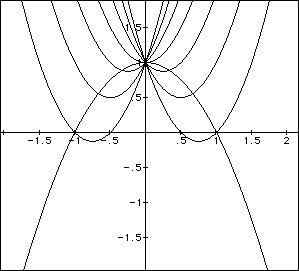
It is clear that locus's graph is not the one we are looking for. So
we should change
The following graph shows that this is now the locus of the vertices.
In general, if we consider the equation
and would like to find the locus of the vertices, we need to consider
both the a term and the c term. The b term ,as long as a and c remains the
same, will just cause a shift of the parabola with the vertex remaining
on the locus of vertices determined by a and c.
Consider the equation
Now graph this relation in the xb plane. We get the following graph.
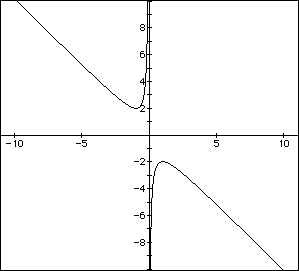
If we take any particular value of b, say b=3, and overlay this equation
on the graph we add a line parallel to the x- axis. If it intersects the
curve in the xb plane the intersection points correspond to the roots of
the original equation for that value of b. we have the following graph.
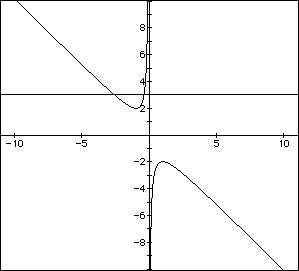
For each value of b we select, we get a horizontal line. It is clear
on a single graph that we get two negative real roots of the original equation
when b > 2 , on e negative real root when b=2, no real roots for -2 <
b < 2, one positive real root when b=-2, and two positive real root when
b=-2, and two positive real roots when b < -2.
Consider the case when c=-1 rather than +1.
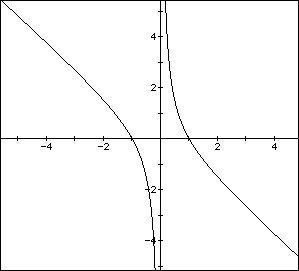
What we notice is that there is no value for b that will not have two
roots, and one of the roots must be positive and one must be negative. This
due to the c term at the end being negative. For two number two multiply
together and give use a negative one must be positive and the other negative.
In the following example
is considered. If the equation is graphed in the xc plane, it is easy
to see that the curve will be a parabola. For each value of c considered,
its graph will be a line crossing the parabola in 0, 1, or 2 points-- the
intersections being at the roots of the original equation at that value
of c. In the graph, the graph of c=1 is shown. The equation
will have two negative roots--approximately -0.2 and -4.8.
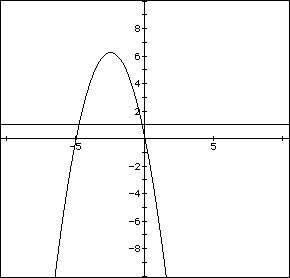
There is one value of c where the equation will have only 1 real root--
at c=6.25. For c > 6.25 the equation will have no real roots and for
c < 6.25 the equation will have two teal roots, both negative for 0 <
c < 6.25, one negative and one 0 when c=0 and one negative and one positive
when c < 0.
The question at this point is why is there no real roots for c > 6.25.
We need to consider the x value at this point and how is corresponds to
the b value. The x value for c=6.25 is -2.5. This is exactly 1/2 of the
b coefficient of 5. This would lead us to believe that for an equation in
the form
that there will not be any real roots for c value that corresponds to
an b value that is larger than 1/2 the value of b. Take for example the
equation
We will not be able to have a real root for any c that has a corresponding
x value that is larger than 4.5.
If we consider the family of parabolas that is graphed for
with the use of several values for b such as b=9, 8, 6, 3, and look at
the graph the will generate the locus of all the values for which is the
maximum value for which c will have a real root . The equation
will create these maximums.
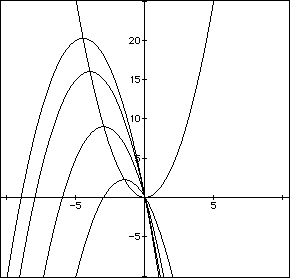
The use of these two equation together will allow use to know before
we ever graph if the c value we are considering has a real root.