Some of you may have experienced some problems with sketching your graphs in the tasks of unit 3 since your graphing devices may have wanted you to give the equation in the form y = ..., that way you would have ultimately had to draw two graphs (equations below for unit 3 - task 1) to get the illusion of the orbit and the Earth in your sketch.
![]() or
or ![]() (Unit 2, task 1)
(Unit 2, task 1)
The Cartesian representation of the ellipse has one further shortcoming for the application of space flight. In space flight and in particular the scenario we have sketched, it is critical to know exactly where the vehicle is at any point in time (both if you are trying to avoid it and if you are trying to meet it!). The Cartesian representation has the limitation that for any value of x there are two corresponding values for y and for every value of y there are two corresponding values of x (with the exception of the apogee, perigee and nodes), so in the application of space flight even knowing one of the coordinates and given the representation of the orbit in Cartesian form only narrows the position of the vehicle down to two possible place (which are more than likely very far apart!).
One way of addressing this matter is to use a different representation for the ellipse, there is one that we will consider, the polar representation.
We are familiar with finding a point in the plane by specifying its rectangular coordinates (x, y). In space flight (and other applications) for reasons including those sited above it is often more useful to locate points by means of their polar coordinates. The polar coordinates of a point give its position relative to a fixed reference point O (the pole) and a given ray beginning at O (the polar axis). To start with let us consider the familiar x-y plane and let O be the origin and the positive x-axis the polar axis, then the point P with polar coordinates r and t (where t is often given as the angle theta) written (r, t) is located as follows:
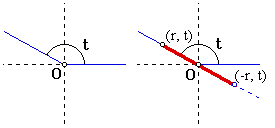 First find the angle t (measured counter-clockwise) with the positive
x-axis as one side, then
First find the angle t (measured counter-clockwise) with the positive
x-axis as one side, then
It may (or may not be interesting) to visit a discussion of trigonometric graphs drawn using polar coordinates that I prepared during a class that I took at the University of Georgia (visit the discussion).
We are now ready to describe the ellipse by means of polar coordinates. To do this we will use the second definition used in unit 2 namely:
A conic section with eccentricity e is the locus of a point P whose distance from the focus (F) is e times its distance from the directrix.
We begin by finding the general equation for a conic in polar coordinates:
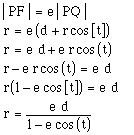
Note when the directrix goes through (d; 0) the equation becomes: ![]()
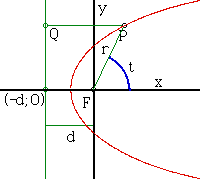
 If we now consider the figure alongside for the ellipse (with e<1)
and use the equations derived above then:
If we now consider the figure alongside for the ellipse (with e<1)
and use the equations derived above then:
for t = 0 we get ![]() and t = pi we get
and t = pi we get ![]()
furthermore ![]() which implies
which implies ![]()
and we get the following equations for an ellipse with eccentricity e, major axis a and focus at the origin:
or
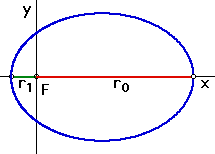
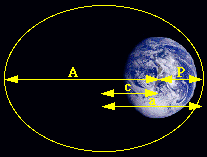 What remains to do before we can use the equation just derived is to
see if we can find the eccentricity e for an ellipse using no more information
than we previously used to draw the ellipses, that is given the apogee
and perigee alone.
What remains to do before we can use the equation just derived is to
see if we can find the eccentricity e for an ellipse using no more information
than we previously used to draw the ellipses, that is given the apogee
and perigee alone.
Determine e in terms of A and P alone.
 Go to unit
5,
Go to unit
5,  return to welcome
page.
return to welcome
page.