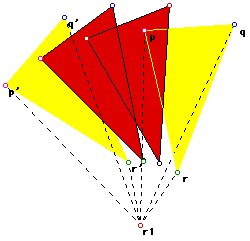
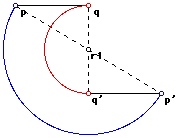
fig 1: p, q, and r have been rotated through n1 degrees
with r1 as the center of rotation.
While studying transformational geometry (MAT 722) we come across the
following situation:
Does the set S of rotations (in RxR) about any point in RxR form a group
(under composition)?
The first matter to be established is whether or not the set is group is
closed. Here follows a geometric discussion of this question:
1. Consider and three points p, q and r in the plane.
2. Consider another point r1 in the plane.
3. Let us define ro1 as the rotation of points p, q and r through n1 degrees
(anti-clockwise) with r1 as center.

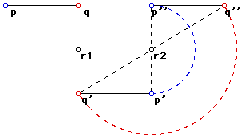
4. Let us now introduce a second center of rotation r2 and rotate the
products of ro1 (namely p', q' and r') through n2 degrees in an anti-clockwise
direction:
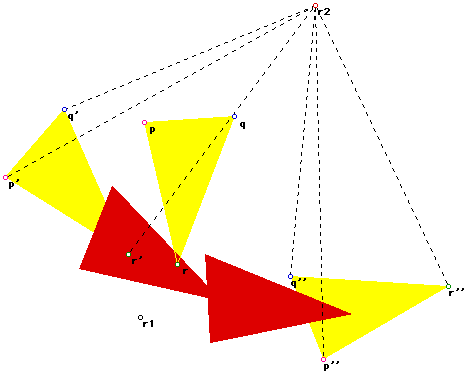
For the set S to be a group, we must show that it is closed under the
operation (in this case rotation about any point). Rephrased we need to
show that there exists a single rotation that can move r, p and q to r'',
p'' and q''.
Let us see if this rotation can be found:
The center of the rotation moving p to p'' will lie on the perpendicular
bisector of the the line segment joining p and p'', similarly the center
of the rotation moving q to q'' will lie on the perpendicular bisector of
the the line segment joining q and q'' and similarly the center of the rotation
moving r to r'' will lie on the perpendicular bisector of the the line segment
joining r and r''.
Let us construct these perpendicular bisectors:
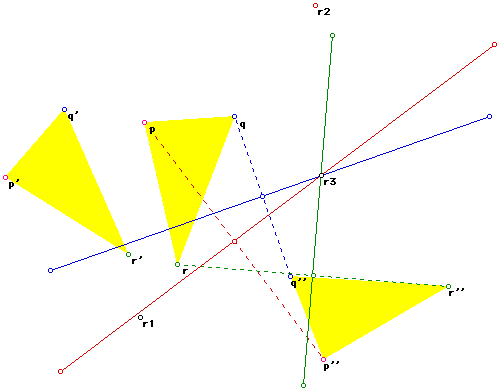
A first glance would suggest that these perpendicular bisectors are concurrent
and so we can rotate pqr around the point r3 and get p''q''r''........
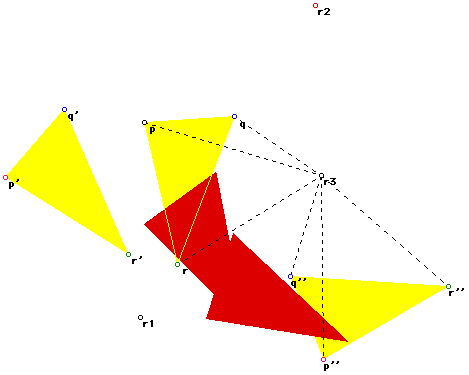
If you have Geometers' Sketchpad you may wish to click
here for an animated show of the rotations shown piecewise in the
figures above.
Will this always hold........
Well the diagram is convincing, furthermore we can manipulate the Geometers'
Sketchpad figure in a number of different ways and the property remains
as shown.....
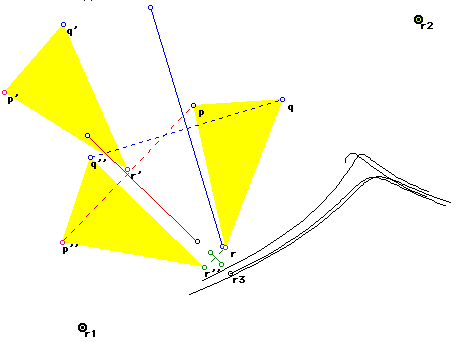
Now we select another point r2 and we rotate the point p' and q' about
r2 (also through 180 degrees):
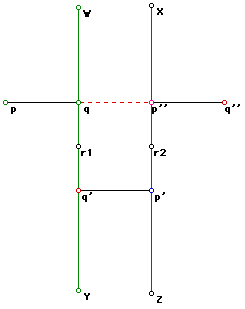
Following the earlier argument in this discussion, it remains to find
a point r3 that will rotate p to p'' and q to q''. This point will be found
at the intersection of the perpendicular bisectors joining p to p'' and
q to q''...........
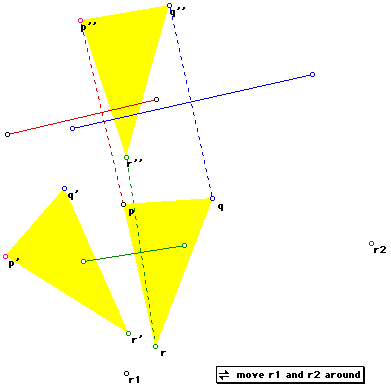
Well - it would appear as if we have a case for which no r3 can be found.
Hence the claim that rotations of the plane about any centre are closed
is false.
Why did we not pick up this problem with the Geometers' Sketchpad
figure discussed at first?? It may be argued that we had a special case
or, and I subscribe to this idea, we were not sufficiently sensitive to
the information in the diagram.....
We now return to fig. 3 and this time we use Geometers' Sketchpad
to move the points r1 and r2 around using the animation function (click
here to see a demonstration).
One result of this animation is........
It may be argued that the perpendicular bisectors do intersect but the
intersection is not on the page - to address this comment we return to the
diagram and use the trace funtion of Geometers' Sketchpad to trace
the path of r3 as it moves about under transformation (click
here to see a demonstration).
One result of this trace is shown below......
Conclusion
Our Geometers' Sketchpad DID demonstrate the claim that rotations
of the plane about any centre are closed is false. At first, however, we
did not explore the messages sufficiently.