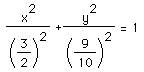
Prepare a construction using the following steps:
1) Construct a circle.
2) Construct a point inside the circle.
3) Construct a point on the circle.
4) Construct a segment connecting the point on the circle and the point inside the circle.
5) Construct the midpoint and perpendicular bisector of that segment. Trace the locus of the perpendicular bisector as the point on the circle moves around the circle. Use an "animate" button.
6) Make a script for future use.
7) Test your script several times to make sure that it works.
8) Drag the point inside the circle closer to the center. What can you say about the changes?
9) Drag the point inside the circle further away from the center. What can you say about the changes?
10) Drag the point inside the circle onto the circle. What can you say about the changes?
11) Drag the point inside the circle to the center. What can you say about the changes?
1) If C is not inside the circle after the construction, drag C inside.
2) Construct the segment connecting the point on the circle and the center.
3) Construct the point of intersection of the perpendicular bisector and the new segment.
4) Trace the locus of this point as the point on the circle moves around the circle. Use an "animate" button.
5) What can you say about this point that you traced?
6) What figure seems to appear?
7) Prove your conjecture. (Hint : Connect this point and the point inside the circle. Use congruent triangles.
1) Construct a line and hide its control points.
2) Construct points A, B, and C on the line with C between A and B.
3) Hide the line and construct line segments AC, CB, and AB.
4) Construct and label points F1 and F2.
5) Construct a circle with center F1 and radius AC. Construct another circle with center F2 and radius CB. Drag B until the two circles intersect
6) Trace the two intersection points as C moves along segment AB using an animation button.
7) What shape appears to be formed by the trace?
8) Prove your conjecture.
9) Move F1 and F2 to different locations and see how the figure changes.
10) Assume A and B remain fixed. How far apart can F1 and F2 be moved before the figure can no longer be formed?
1) Snap to grid.
2) Place F1 on the point (-2,0) and F2 on the point (2,0).
3) Make the length of AB 5 units.
4) Animate.
5) Using your knowledge of the equations of ellipses, what do you think the equation of this ellipse will be?
6) Use Algebra expressor to test your conjecture.
7) Copy and paste your graph onto the graph you just created in GSP.
8) Adjust your scale by using the unit point and drag your grid if nescessary.
9) Make any adjustments in the placement of the centers of the circle to coincide with your previous instructions in 2 and 3 above.
10) Animate your GSP construction to see if the two ellipses coincide. Save this as a file called "Snap to Grid".
1) Graph :
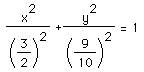
2) Copy your graph GSP.
3) Snap to grid and adjust the scale as you did in part IV.
4) Construct an ellipse using the concepts of the two-pins-and-a-string construction from part IV above which will generate this ellipse.
5) Where do you need to place the foci (centers of your circles F1 and F2)?
6) How long is your segment AB? What does this relate to the general equation of an ellipse :
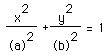
1) Construct circle A.
2) Construct an arbitrary point C inside circle A.
3) Construct circle C inside circle A.
4) Construct a point F on circle A.
5) Construct line AF.
6) Construct a radius for circle C.
7) Construct circle F with the same radius as circle C.
8) Constuct the intersaection, point H, of line AF and Circle F.
9) Construct segment CH.
10) Constuct the perpendicular bisector of CH. Name the midpoint I.
11) Construct the intersection, point J, of the perpendicular bisector and line AF.
12) Trace J as F animates around circle A.
13) What figure seems to be traced? Prove your conjecture.