The following ideas are presented in the video series "PROJECT Mathematics." This essay is accompanied with GSP files which are similar to the animation sequences on the tape "SINES AND COSINES PART II." The purpose of these files is so that students investigate the situation that were presented on the video tape.

First consider the Pythagorean theorem:

Given a right triangle, then the square of the side opposite of the right angle is equal to sum of the squares of the other sides.

The following demonstration is based on Euclid's proof.

(Click here.)

An interesting fact about Euclid's proof, as opposed to the proof using similar triangles, is that Euclid's proof shows that areas of the little squares add up to the areas of the big square. The proof using similar requires the existence of square root, which can be irrational. Euclid's proof does not need square roots.

Now what happens when the same demonstration is attempted on an arbitrary triangle.

(Click here.)

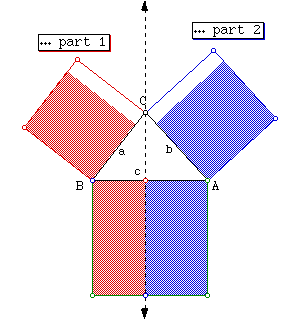
In this case the two rectangles do not fill up the corresponding squares, meaning the sum of the squares of the two smaller sides is greater than the larger side squared. But how much larger?

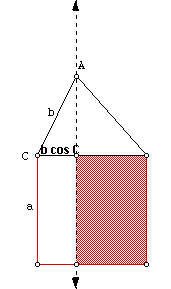
So we need to find the area of the white rectangle which is

(a)(b cos C).

Strangely enough the white rectangle in the other square is also

(a)(b cos C).

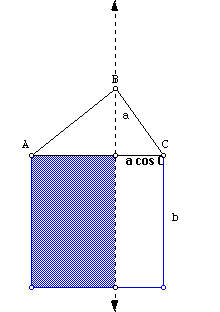
So,

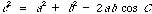
or the law of cosines.