

Palindromes were first used in language to define words or lines that read the same backwards or forward. The word is of Greek origin coming from "palin dromo" which translates approximately to "to read back again." Examples of palindromes include:
They have also been called Sotadics after their reputed inventor Sotades, a Greek poet who lived around 300BC. Palindromic words were also used in other languages including English. The longest palindrome in English probably is:
Two other well known palindromes are
and Napoleon's famous reputed quotation:
One of the most celebrated palindrome is the Greek word
The word means "wash my transgressions not my face".
Palindromic numbers like palindromic words or lines obey the same property of being the same whether they are read from left to right or vice-versa. Examples include:
Palindromes could be formed from a number that is not a palindrome by adding the original number to the number formed by reversing the digits. For example:
which is a palindrome. Sometimes, however, more than one reversal is necessary. Thus,
which is not a palindrome. But
is a palindrome.
Writing in the Arithmetic Teacher of January 1985, Clarence J. Dockweiler in an article entitled "Palindromes and the laws of 11" made the following observation:
"If in the process of obtaining a palindrome, a sum with an even number of digits is obtained, the palindrome will be a multiple of 11."
He warned, however, that he was not sure that every number could be turned into a palindrome.
This researcher independently observed that palindromes with an even number of digits were divisible by 11 and set out to prove that all such palindromes, whether they arose from the reversal-sum process or not, were divisible by 11.
A general six-digit palindrome will be chosen but the results will be generalized to include all even numbered palindromes. The method of Induction will be used to verify the hypothesis.
Consider the palindrome
This could be written as
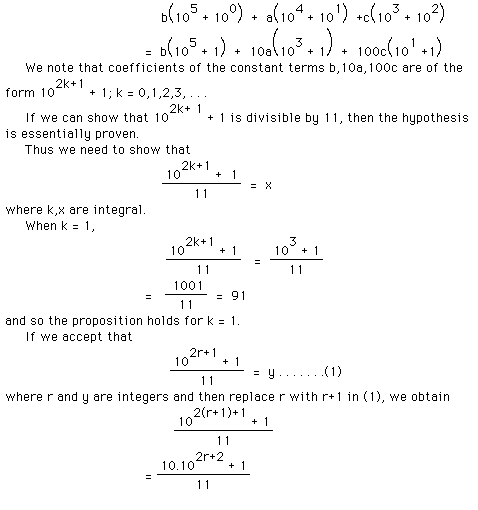

The following spreadsheet shows what happens when we divide palindromes
with an even number of digits by 11. The palindromes were created by using
the relationship established earlier. Six-digit palindromes can be created
by the relationship:
![]()
where a,b,c all lie between 0 and 9.
In the first, second, and third columns we have values of a,b,and c. In the fourth column we have the palindromes formed by using the relationship above and in the fifth column we have the results obtained when we divide the palindromes by 11. Note that we have an integral answer every time.
It is also interesting to note that those palindromes with digits that increase from the left and then decrease appropriately as we get to the middle digit(s) have palindromic quotients when they are divided by 11!
1 1 1 111111 10101 1 1 2 112211 10201 1 1 3 113311 10301 1 1 4 114411 10401 1 1 5 115511 10501 1 1 6 116611 10601 1 1 7 117711 10701 1 1 8 118811 10801 1 1 9 119911 10901 1 2 1 211112 19192 1 2 2 212212 19292 1 2 3 213312 19392 1 2 4 214412 19492 1 2 5 215512 19592 1 2 6 216612 19692 1 2 7 217712 19792 1 2 8 218812 19892 1 2 9 219912 19992 1 3 1 311113 28283 1 3 2 312213 28383 1 3 3 313313 28483 1 3 4 314413 28583 1 3 5 315513 28683 1 3 6 316613 28783 1 3 7 317713 28883 1 3 8 318813 28983 1 3 9 319913 29083 1 3 1 311113 28283 1 3 2 312213 28383 1 3 3 313313 28483 1 3 4 314413 28583 1 3 5 315513 28683 1 3 6 316613 28783 1 3 7 317713 28883 1 3 8 318813 28983 1 3 9 319913 29083 1 4 1 411114 37374 2 4 1 421124 38284 3 4 1 431134 39194 4 4 1 441144 40104 5 4 1 451154 41014 6 4 1 461164 41924 7 4 1 471174 42834 8 4 1 481184 43744 9 4 1 491194 44654 5 1 1 151151 13741 5 1 2 152251 13841 5 1 3 153351 13941 5 1 4 154451 14041 5 1 5 155551 14141 5 1 6 156651 14241 5 1 7 157751 14341 5 1 8 158851 14441 5 1 9 159951 14541 6 1 1 161161 14651 6 1 2 162261 14751 6 1 3 163361 14851 6 1 4 164461 14951 6 1 5 165561 15051 6 1 6 166661 15151 6 1 7 167761 15251 6 1 8 168861 15351 6 1 9 169961 15451 7 1 1 171171 15561 7 1 2 172271 15661 7 1 3 173371 15761 7 1 4 174471 15861 7 1 5 175571 15961 7 1 6 176671 16061 7 1 7 177771 16161 7 1 8 178871 16261 7 1 9 179971 16361 8 1 1 181181 16471 8 1 2 182281 16571 8 1 3 183381 16671 8 1 4 184481 16771 8 1 5 185581 16871 8 1 6 186681 16971 8 1 7 187781 17071 8 1 8 188881 17171 8 1 9 189981 17271 9 1 1 191191 17381 9 1 2 192291 17481 9 1 3 193391 17581 9 1 4 194491 17681 9 1 5 195591 17781 9 1 6 196691 17881 9 1 7 197791 17981 9 1 8 198891 18081 9 1 9 199991 18181 1 5 1 511115 46465 1 5 2 512215 46565 1 5 3 513315 46665 1 5 4 514415 46765 1 5 5 515515 46865 1 5 6 516615 46965 1 5 7 517715 47065 1 5 8 518815 47165 1 5 9 519915 47265 1 6 1 611116 55556 1 6 2 612216 55656 1 6 3 613316 55756 1 6 4 614416 55856 1 6 5 615516 55956 1 6 6 616616 56056 1 6 7 617716 56156 1 6 8 618816 56256 1 6 9 619916 56356 1 7 1 711117 64647 1 7 2 712217 64747 1 7 3 713317 64847 1 7 4 714417 64947 1 7 5 715517 65047 1 7 6 716617 65147 1 7 7 717717 65247 1 7 8 718817 65347 1 7 9 719917 65447
Benet's Readers Enclycopaedia, (1987). Harper and Row
Dockweiler, C.J. (1985). Palindromes and the "Law of 11". Arithmetic Teacher, 32(5)